Bài1;aChứng minh rằng nếu 2 số dương có tích không đổi thì tổng của chúng nhỏ nhất khi và chỉ khi hai số đó bằng nhau
b;áp dụng tìm min của các biểu thức sau với x>0
A=(x4+4x3 + 4x2 + 9) /(x2 + 2x)
B=(x^2 + 2x+3)(x^2 + 2x+9)/(x^2 + 2x+1)
Giúp mình với, mình cần gấp, rất gấp. đúng mình tick cho







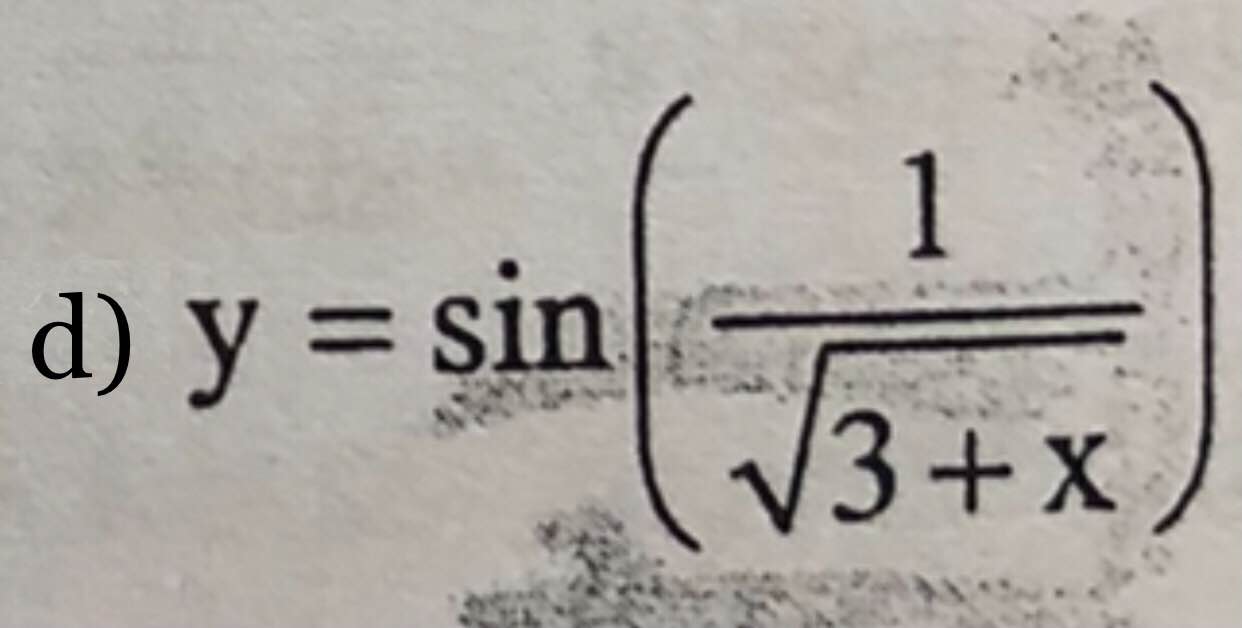
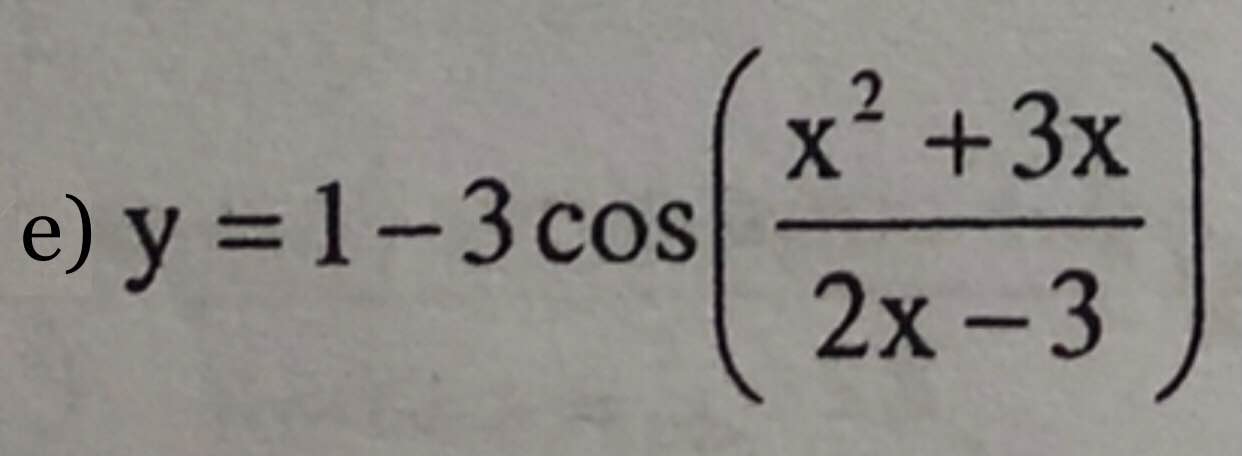
gọi xy=k^2 với k là hằng số.
Ta có: [(x+y)/2]^2 >=xy <=>(x+y)^2 >= 4xy <=> (x+y) >= 2k =>min(x+y)=2k<=>x=y=k.
a)Xét hai số dương tích bằng a( với a là hằng số):
ta có (x+y)^2 >= 4xy=4a <=> x=y
Vì x,y >0 nên x+y nhỏ nhất <=> x=y.