tam giacs ABC có AB=9, BC=10,CA=11. Gọi M là trung điểm của BC và N là trung điểm của AM. Tính độ dài BN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(BM=\dfrac{1}{2}BC=3\)
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cos60^0}=\sqrt{19}\)
\(BN=\dfrac{\sqrt{2\left(AB^2+BM^2\right)-AM^2}}{2}=\dfrac{7}{2}\)

tự vẽ hình nhé
a) ta có: tam giác ABC cân tại A
,mà MB=MC
=> AM LÀ đg phân giác
=> am VUÔNG GÓC VỚI BC
b) AM là đg phân giác (cmt)
=> AM =1/2 BC= 9:2=4.5(cm)
c) ta có tam giác AMB là tam giac vuông (AM vuông góc với BC )
mà N là trg điểm của AB
=>MN là đg phân giác
=> MN=1/2AB=7.5:2=3.75(cm)
d)ta có: AB=AC=7.5(cm)
=>AB vuông với AC
mà MN vuông với AB
=>MN//AC
TK DÙM MINK NHOA

Áp dụng định lý Pitago trong tam giác vuông ABC ta có: Từ đây suy ra Lại có M là trung điểm của AC nên |
Gọi I là trung điểm của BC, G là giao điểm của AI và BM, suy ra G là trọng tâm tam giác ABC, suy ra BM = 3GM (1). Do ABC là tam giác vuông nên AI = IB = IC, do đó tam giác IAC là tam giác cân tại I, suy ra Lại có AM = MC (3).
Từ (2), (3) và (4) suy ra Suy ra GM = NM (5). Từ (1) và (5) suy ra BM = 3NM (đpcm). |
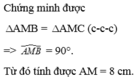
Theo công thức đường trung tuyến:
\(AM^2=\dfrac{AB^2+AC^2}{2}-\dfrac{BC^2}{4}=\dfrac{9^2+11^2}{2}-\dfrac{10^2}{4}=76\Rightarrow AM=2\sqrt{19}\)
\(BN^2=\dfrac{AB^2+BM^2}{2}-\dfrac{AM^2}{4}=\dfrac{9^2+\dfrac{1}{4}.10^2}{2}-\dfrac{76}{4}=34\Rightarrow BN=\sqrt{17}\)
đề có thiếu dữ kiện ko