Cho hình vuông có cạnh bằng 15cm. Trên cạnh AB lấy điểm M sao cho diện tích
tam giác AMD bằng 1/3 diện tích hình vuông ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

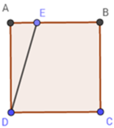
Gọi BE = x (m).
Diện tích hình vuông ABCD là: SABCD = AB2 = 202 = 400 (m2)
Diện tích hình thang vuông BCDE là:
SBCDE = ( B E + D C ) B C 2 = ( x + 20 ) .20 2 = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng 3 4 diện tích hình vuông ABCD nên ta có:
SBCDE = 3 4 SABCD = 10(x + 20) = 3 4 .400 óx + 20 = 30 ó x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Đáp án cần chọn là: D

( HÌNH ẢNH CHỈ MANG TÍNH CHẤT MINH HỌA CHO SẢN PHẨM )
SAMND = MBCN = 1 / 2 SABCD ( VÌ AM = NC ; MB = DN VÀ CÓ CHUNG CHIỀU CAO LÀ CHIỀU RỘNG CỦA HÌNH CHỮ NHẬT )
S AMND HAY S MBCN LÀ : 54: 2= 27 ( CM2 )
AM = 1/3 AB HAY AM = 1/2 MB SUY RA NC = 1/2 MB
S BNC = 1/2 S MBN = 1/3 S MBCN ( VÌ NC = 1/2 M VÀ CÓ CHUNG CHIỀU CAO VỚI HÌNH THANG MBCN )
S BNC LÀ : 27 : 3 = 9 ( CM 2 )
TA THẤY :
CK = 1/2 MG ( VÌ S BCN = 1/2 MBN VÀ CÓ CHUNG CẠNH BN)
S INC = 1/2 MNI = 1/3 MCN ( CK = 1/2 MG VÀ CÓ CHUNG CẠNH NI )
SMCN = SNBC ( VÌ CÓ CHUNG CẠNH ĐÁY NC VÀ CÓ CHUNG CHIỀU CAO )
S ICN LÀ : 9:3 = 3 (CM2 )
ĐÁP SỐ
ĐÙNG KHÔNG ? ??
Yêu cầu đề bài là gì vậy bạn? Nếu là tìm diện tích tam giác $AMD$ thì:
$S_{AMD}=\frac{1}{3}S_{ABCD}=\frac{1}{3}.15.15=75$ (cm2)