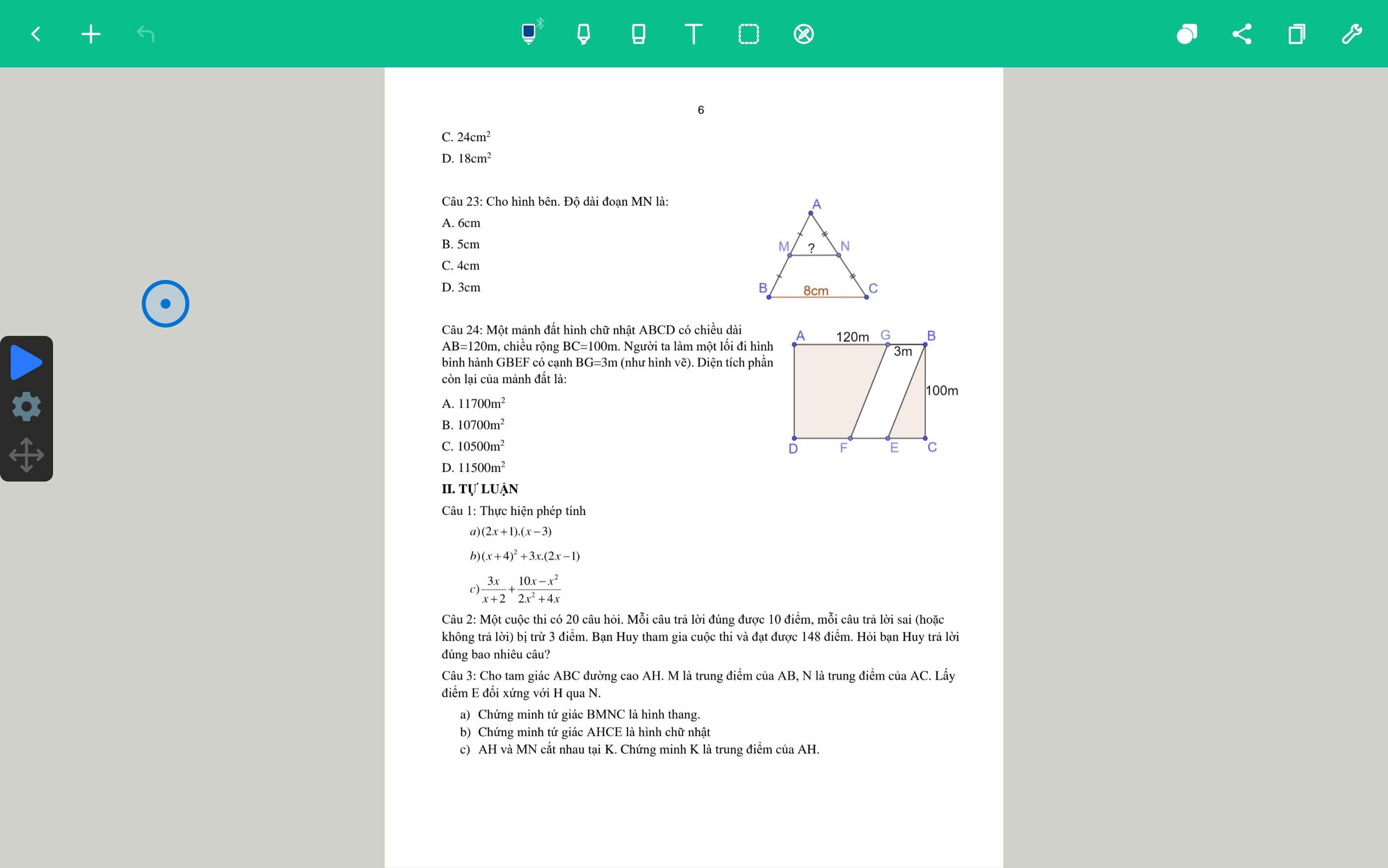
Giải cho em bài 24, có đáp án và lời giải chi tiết nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2021
\(\left(a-b\right)^2=a^2-2ab+b^2=144\\ \Leftrightarrow154-2ab=144\\ \Leftrightarrow ab=5\\ \Leftrightarrow M=\left(a-b\right)^3+3ab\left(a-b\right)=12^3+3\cdot5\cdot12=1908\)
22 tháng 12 2018
Giải
a+b+c = abc (1)
Trường hợp 1 : a.b.c = 0 ⇒⇒ a+b+c = 0 mà a, b, c ≥0≥0 ⇒⇒ a=b=c=0 ( thỏa mãn )
Trường hợp 2 a.b.c > 0 ⇒⇒ a, b, c > 0
Vì vai trò của a, b, c bình đẳng nên có thể giả sử a≤b≤ca≤b≤c ⇒⇒ abc = a + b + c ≤≤ 3c ⇒⇒ ab ≤≤ 3 ( vì c> 0 )
Mà a≤ba≤b nên a2≤ab≤3a2≤ab≤3 ⇒⇒ a = 1
Thay a = 1 vào (1) ta có b+c+1 = bc ⇔⇔ (b-1) (c-1) = 2
Mà 0≤b−1≤c−10≤b−1≤c−1 nên b-1 = 1, c-1 =2 ⇒⇒ b=2, c= 3
Thử lại thấy đúng ⇒⇒ (a, b, c) = (0, 0, 0) , (1, 2 , 3) , (1, 3, 2), ( 2, 1, 3) , ( 2, 3, 1 ) , ( 3, 1, 2 ) , ( 3, 2, 1 )
Bạn tham khảo nhé
MM
3
28 tháng 5 2022
\(\Leftrightarrow\left(x^2-x\right)^2-x^2+x-30=0\)
\(\Leftrightarrow\left(x^2-x\right)^2-\left(x^2-x\right)-30=0\)
\(\Leftrightarrow\left(x^2-x-6\right)\left(x^2-x+5\right)=0\)
\(\Leftrightarrow x^2-x-6=0\)
=>(x-3)(x+2)=0
=>x=3 hoặc x=-2
KS
28 tháng 5 2022
`(x^2 -x)^2 +x=x^2 +30`
`<=>(x^2 -x)^2 -(x^2 -x)-30=0`
Đặt `t=x^2 -x`
`t^2 -t-30=0`
`<=>t^2 -6t+5t-30=0`
`<=>t(t-6)+5(t-6)=0`
`<=>(t-6)(t+5)=0`
`<=>[(t-6=0),(t+5=0):}`
`<=>[(x^2 -x-6=0),(x^2 -x+5=0):}`
`<=>x^2 -x-6=0`
`<=>x^2 -3x+2x-6=0`
`<=>x(x-3)+2(x-3)=0`
`<=>(x-3)(x+2)=0`
`<=>[(x-3=0),(x+2=0):}`
`<=>[(x=3),(x=-2):}`
Vậy `S={-2;3}`
KN
2
KN
0
EU
giúp em 2 bài nha bài 21 lời giải còn bài 20 ko lời giải chỉ đáp án
2
Câu 24: B