tìm Timf Tìm tìm các số nguyên x và y sao cho(x-3) x (x+y) = 7các số nguyên x và y sao cho (x-3)(x+y)=7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H1
1
20 tháng 7 2020
Bài làm:
Ta có: \(\left(x-3\right)\left(x+y\right)=-7\)
Mà \(-7=1.\left(-7\right)=\left(-7\right).1\)nên ta xét 4 trường hợp sau:
+TH1: \(\hept{\begin{cases}x-3=1\\x+y=-7\end{cases}\Leftrightarrow}\hept{\begin{cases}x=4\\y=-11\end{cases}}\)
+TH2: \(\hept{\begin{cases}x-3=-7\\x+y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x=-4\\y=5\end{cases}}}\)
+TH3: \(\hept{\begin{cases}x-3=-1\\x+y=7\end{cases}\Leftrightarrow}\hept{\begin{cases}x=2\\y=5\end{cases}}\)
+TH4: \(\hept{\begin{cases}x-3=7\\x+y=-1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=10\\y=-11\end{cases}}\)
Vậy ta có 4 cặp số \(\left(x;y\right)\)thỏa mãn: \(\left(4;-11\right)\), \(\left(-4;5\right)\), \(\left(2;5\right)\), \(\left(10;-11\right)\)
PN
0
QC
6 tháng 3 2020
a )
(x-3).(2y+1)=7
(x-3).(2y+1)= 1.7 = (-1).(-7)
Cứ cho x - 3 = 1 => x= 4
2y + 1 = 7 => y = 3
Tiếp x - 3 = 7 => x = 10
2y + 1 = 1 => y = 0
x-3 = -1 ...
6 tháng 3 2020
1.tìm các số nguyên x và y sao cho:
(x-3).(2y+1)=7
Vì x;y là số nguyên =>x-3 ; 2y+1 là số nguyên
=>x-3 ; 2y+1 C Ư(7)
ta có bảng:
| x-3 | 1 | 7 | -1 | -7 |
| 2y+1 | 7 | 1 | -7 | -1 |
| x | 4 | 10 | 2 | -4 |
| y | 3 | 0 | -4 | -1 |
Vậy..............................................................................
2.tìm các số nguyên x và y sao cho:
xy+3x-2y=11
x.(y+3)-2y=11
x.(y+3)-y=11
x.(y+3)-(y+3)=11
(x-1)(y+3)=11
Vì x;y là số nguyên => x-1;y+3 là số nguyên
=> x-1;y+3 Thuộc Ư(11)
Ta có bảng:
| x-1 | 1 | 11 | -1 | -11 |
| y+3 | 11 | 1 | -11 | -1 |
| x | 2 | 12 | 0 | -10 |
| y | 8 | -2 | -14 | -4 |
Vậy.......................................................................................
PN
0
PM
3
S
20 tháng 7 2019
Bn tham khảo link này nha :
https://olm.vn/hoi-dap/detail/2023570570.html
~Study well~
#KSJ
CC
20 tháng 7 2019
Vì \(\frac{3+x}{7+y}=\frac{3}{7}\)\(\Rightarrow\)( 3 + x) . 7 = (7+y) . 3
=> 21 + 7x = 21 + 3y
=> 7x = 3y (1)
Vì x + y = 20 => 3( x + y) = 60
=> 3x + 3y = 60
=> 3y = 60 - 3x (2)
Từ (1) và (2) => 7x = 60 -3x
=> 7x + 3x = 60 => 10x = 60 => x = 6
=> y = 20 - 6 = 14
KL :...
TT
2
2 tháng 3 2020
\(a.x=1;y=9\)
\(b. (x-6). (y+2)=7\)
Ta lập bảng :
| \(x-6\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(y+2\) | \(7\) | \(-7\) | \(1\) | \(-1\) |
| \(x \) | \(7\) | \(5\) | \(13\) | \(-1\) |
| \(y\) | \(5\) | \(-9\) | \(-1\) | \(-3\) |
\(Vậy :..........\)
LT
2 tháng 3 2020
a) Vì x, y nguyên mà x.y = 9 nên x, y thuộc Ư(9)
Mà x< y. Ta có bảng sau
| x | 1 | -9 |
| y | 9 | -1 |
Vậy (x,y) \(\in\){(1;9) , ( -9; -1) }
b) vì x, y nguyên suy ra x-6 , y + 2 nguyên
mà (x-6). ( y+2) =7
nên (x-6), ( y+2) thuộc Ư(7) .Ta lập bảng như sau
| x-6 | 1 | -1 | 7 | -7 |
| y+2 | 7 | -7 | 1 | -1 |
| x | 7 | 5 | 13 | -1 |
| y | 5 | -9 | -1 | -3 |
Tự kết luận nhé
PT
1
9 tháng 2 2021
a) Ta có: (x-3)(y+2)=5
nên (x-3) và (y+2) là ước của 5
\(\Leftrightarrow x-3;y+2\in\left\{1;-5;-1;5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-3=1\\y+2=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=3\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-3=5\\y+2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=-1\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-3=-1\\y+2=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-7\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-3=-5\\y+2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-3\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(4;3\right);\left(8;-1\right);\left(2;-7\right);\left(-2;-3\right)\right\}\)
b) Ta có: (x-2)(y+1)=5
nên x-2 và y+1 là các ước của 5
\(\Leftrightarrow x-2;y+1\in\left\{1;-1;5;-5\right\}\)
Trường hợp 1:
\(\left\{{}\begin{matrix}x-2=1\\y+1=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Trường hợp 2:
\(\left\{{}\begin{matrix}x-2=5\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\)
Trường hợp 3:
\(\left\{{}\begin{matrix}x-2=-1\\y+1=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-6\end{matrix}\right.\)
Trường hợp 4:
\(\left\{{}\begin{matrix}x-2=-5\\y+1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\left\{\left(3;4\right);\left(7;0\right);\left(1;-6\right);\left(-3;-2\right)\right\}\)
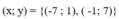
Đề đây ạ:
Tìm các số nguyên x và y sao cho (x-3)(x+y)=7