helpppppppppp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 5 2022
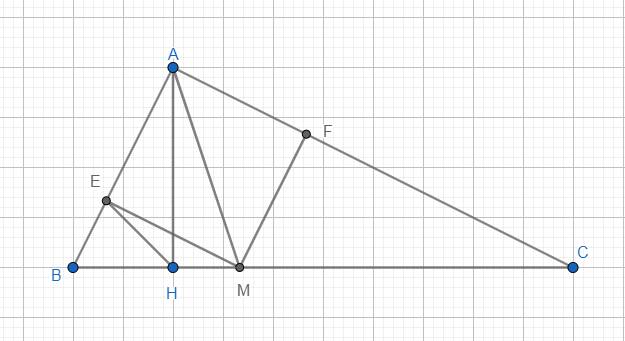
a) Xét △BEM và △BHA có:
\(\hat{B}\): chung
\(\hat{BEM}=\hat{BHA}\) = 90o
Do đó: △BEM đồng dạng △BHA (gg)
=> \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\) => BE.BA = BH.BM
b) Theo câu a), ta có:
BE.BA = BH.BM
=> \(\dfrac{BE}{BM}=\dfrac{BH}{BA}\)
Lại có: \(\hat{B}\): chung
nên △BEH đồng dạng △BMA (cgc)
=> \(\hat{BHE}=\hat{BAM}\)
Vì AM là tia phân giác của \(\hat{BAC}\) nên \(\hat{BAM}=\dfrac{\hat{BAC}}{2}=\dfrac{90^o}{2}=45^0\)
=> \(\hat{BHE}=45^0\)
mà \(\hat{BHA}=90^o\)
Nên HE là tia phân giác góc AHB.
20 tháng 7 2021
\(\left|2x+1\right|=\left|3x-2\right|\)
\(\Leftrightarrow\)2x-1=3x-2 hoặc 2x-1=-3x+2
\(\Leftrightarrow\)x=1 hoặc x=\(\dfrac{3}{5}\)
Vậy x=\(\left\{1;\dfrac{3}{5}\right\}\)
20 tháng 7 2021
|2x+1|=|3x-2|
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=3x-2\\2x+1=-3x+2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}1=x\\5x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
đúng ko nhỉ :)?
TB
2
DT
1
TC
1
HB
11 tháng 12 2017
3n+4 thuộc BC(5:n+1) nên 3n+4 chia hết cho n+1, 5
3n+4 chia hết cho n+1
3n+4=(3n+3)+1
mà 3n+3=3(n+1) chia hết cho n+1 nên 1 chia hết cho n+1 nên n=0 để 3n+4 chia hết cho n+1
nếu n=0 ta có 3n+4=3.0+4=0+4=4 không chia hết cho 5
nên n thuộc rỗng để 3n+4 thuộc BC(n+1,5)
