Bài 5.2: (2,0 điểm) a) Vẽ hình thoi ABCD biết AB = 65mm và AC = 120mm. Kể tên các trục đối xứng và tâm đối xứng của hình thoi vừa vẽ? b) Một mảnh đất hình bình hành, biết cạnh đáy bằng 23m, mở rộng mảnh đất bằng việc tăng cạnh đáy mảnh đất này thêm 5m thì được mảnh đất hình bình hành mới có diện tích lớn hơn mảnh đất ban đầu là 115m². Tính diện tích mảnh đất hình bình hành ban đầu. Bài 6 (0,5 điểm): Một chiếc máy bay đang bay ở độ cao 7 km so với mực nước biển. Cùng lúc đó, một tầu ngầm lặn ở độ cao -1300 m so với mực nước biển. Tính khoảng cách giữa máy bay và tầu ngầm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khẳng định nào sau đây là sai?
A.Giao điểm của hai đường chéo là tâm đối xứng của hình thoi
B.Hình thoi có những cặp cạnh liên tiếp bằng nhau
C.Hai đường chéo là hai trục đối xứng của hình thoi
D.Hình bình hành luôn là hình thoi(hình thôi 4 cạnh bằng nhau, còn hình bình hành thì ko)


a) Ta có AB = CD (cạnh hình thoi)
BE = DG (gt)
⇒ AB + BE = CD + DG hay AE = CG (cmt)
Xét ΔAHE và ΔCFG có:
AE = CG
∠HAE = ∠FCG (cùng bù với ∠BAD = ∠DCB ),
AH = CF (gt)
Do đó ΔAHE = ΔCFG (c.g.c) ⇒ HE = FG
Chứng minh tương tự ta có HG = EF
Do đó tứ giác EFGH là hình bình hành (các cạnh đối bằng nhau).
b) Nối E và G.
Xét ΔOBE và ΔODG có
BE = DG (gt),
∠OBE = ∠ODG (so le trong),
OB = OD ( tính chất đường chéo của hình thoi ABCD)
⇒ ΔOBE = ΔODG (c.g.c) ⇒ ∠OBE = ∠ODG
Mà ∠DOG + ∠GOB = 180o ⇒ ba điểm G, O, E thẳng hàng.
Chứng minh tương tự ta có H, O, F thẳng hàng.
Vậy O là tâm đối xứng của hình bình hành EFGH.
c) Hình bình hành EFGH là hình thoi ⇔ HE = EF
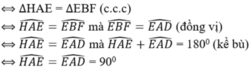
⇔ Hình thoi ABCD có 1 góc vuông
⇔ ABCD là hình vuông.
Vậy hình thoi ABCD phải là hình vuông thì hình bình hành EFGH trở thành hình thoi.

a) Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của BC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay \(MN=\dfrac{8}{2}=4\left(cm\right)\)
Xét tứ giác ACNM có NM//AC(cmt)
nên ACNM là hình thang có hai đáy là NM và AC(Định nghĩa hình thang)
Hình thang ACNM có \(\widehat{CAM}=90^0\)(gt)
nên ACNM là hình thang vuông(Định nghĩa hình thang vuông)
b) Xét tứ giác ABDC có
N là trung điểm của đường chéo BC(gt)
N là trung điểm của đường chéo AD(gt)
Do đó: ABDC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
mà \(\widehat{CAB}=90^0\)(gt)
nên ABDC là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

Trục đối xứng,tâm đối xứng và tâm đối xứng O của hình vuông