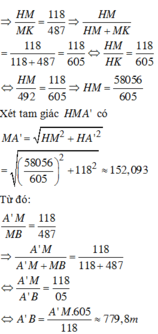Một khúc sông có hai bờ là a , b được coi là song song và khoảng cách giữa hai bờ là AB 325m. Một ca nô dự định đi từ vị trí A sang vị trí B , nhưng do nước chảy xiết nên ca nô đi lệch từ vị trí A đến vị trí C bên bờ sông b hết 1,5 phút với vận tốc trung bình là 18 km/h (tham khảo hình vẽ). Tính góc tạo bởi phương chuyển động của ca nô với bờ sông a (làm tròn kết quả đến độ)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, do nước chảy nên vận tốc ca nô bằng vận tốc dòng nước đẩy ca nô từ B->C =3m/s
\(=>t=\dfrac{300}{3}=100s\)
b,\(=>Vt=\dfrac{400}{100}=4m/s\)
như đã biết quãng AB=400m,quãng AC=300m
theo pytago\(=>AC=\sqrt{AB^2+BC^2}=\sqrt{400^2+300^2}=500m\)
\(=>V\)(so với bờ sông)\(=\dfrac{500}{t}=\dfrac{500}{100}=5m/s\)
Một ca nô đi ngang sông xuất phát từ A nhằm thẳng hướng đến B. A cách B một khoảng AB=400m.Do nước chảy nên ca nô đến vị trí C cách B một đoạn bằng BC=300m.Biết vận tốc nước chảy bằng 3m/s.
a,Tính thời gian ca nô chuyển động.
b,Tính vận tốc của ca no so với nước và so với bờ sông.

Chọn A
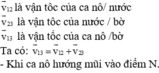
![]()
![]()
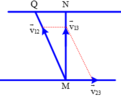
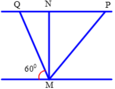
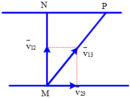
Khi ca nô hướng mũi hướng theo bờ sông góc 60° (v12 và v23 có độ lớn không đổi):
+ Từ hình vẽ:
![]()

Đáp án C
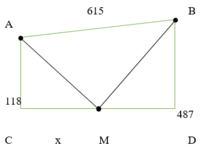
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 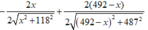
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
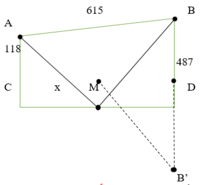
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng

Chọn A.
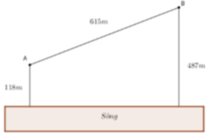
Phương pháp:
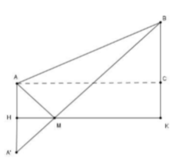
Lấy A’ đối xứng với A qua bờ sông, nối A’B cắt bờ sông tại M khi đó ta có AM + MB = A’B là quãng đường ngắn nhất mà người đó đi.
Sử dụng định lý Pytago và định lý Ta-lét để tính toán.
Cách giải: