Cho hàm số y = f(x) = x2 - 3x - 10
a. Tìm x biết f(x) = -10
b. Tìm x biết f(x) = 0
c. Tìm giá trị nhỏ nhất f(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 4 2019
Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
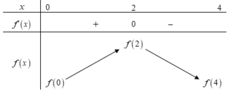
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
CM
9 tháng 3 2017
Ta có bảng biến thiên như hình vẽ sau:
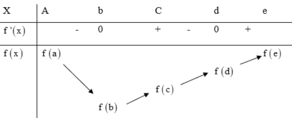
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
NT
1
CM
16 tháng 3 2018
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
7 tháng 2 2021
a) Thay x=-2 vào hàm số f(x)=|3x-1|, ta được:
\(f\left(-2\right)=\left|3\cdot\left(-2\right)-1\right|=\left|-6-1\right|=7\)
Thay x=2 vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(2\right)=\left|3\cdot2-1\right|=\left|6-1\right|=5\)
Thay \(x=-\dfrac{1}{4}\) vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(-\dfrac{1}{4}\right)=\left|3\cdot\dfrac{-1}{4}-1\right|=\left|-\dfrac{3}{4}-\dfrac{4}{4}\right|=\dfrac{7}{4}\)
Thay \(x=\dfrac{1}{4}\) vào hàm số \(f\left(x\right)=\left|3x-1\right|\), ta được:
\(f\left(\dfrac{1}{4}\right)=\left|3\cdot\dfrac{1}{4}-1\right|=\left|\dfrac{3}{4}-1\right|=\dfrac{1}{4}\)
Vậy: f(-2)=7; f(2)=5; \(f\cdot\left(-\dfrac{1}{4}\right)=\dfrac{7}{4}\); \(f\left(\dfrac{1}{4}\right)=\dfrac{1}{4}\)
b) Để f(x)=10 thì \(\left|3x-1\right|=10\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=10\\3x-1=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=11\\3x=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{3}\\x=-3\end{matrix}\right.\)
Để f(x)=-3 thì \(\left|3x-1\right|=-3\)
mà \(\left|3x-1\right|\ge0\forall x\)
nên \(x\in\varnothing\)
a: =>x(x-3)=0
=>x=0 hoặc x=3