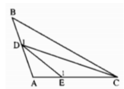
Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm D (khác A và B ), trên cạnh AC lấy điểm E( khác A và C).Chứng minh rằng DE<BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 3 2018
+ ΔADE có ∠E1 là góc ngoài ⇒ ∠E1 > ∠A
Mà ∠A > 90o ⇒ ∠E1 > 90o
ΔCDE có ∠E1 tù ⇒ CD là cạnh lớn nhất ⇒ CD > DE (1)
+ Tương tự xét ΔADC có ∠D1 là góc ngoài
⇒ ∠D1 > ∠A ⇒ ∠D1 > 90o (vì ∠A > 90º)
ΔBDC có ∠D1 tù ⇒ BC là cạnh lớn nhất ⇒ BC > CD (2)
Từ (1) và (2) suy ra BC > DE.
HN
28 tháng 5 2017
Xét \(\Delta CDE\) có \(\widehat{E_1}>\widehat{A}\), mà \(\widehat{A}\) là góc tù nên \(\widehat{E_1}\) là góc tù.
Suy ra CD > DE. (1)
Xét \(\Delta BCD\) có \(\widehat{D_1}>\widehat{A}\) nên \(\widehat{D_1}\) là góc tù. Suy ra BC > CD. (2)
Từ (1) và (2) suy ra BC > DE.
23 tháng 3 2016
Nối C vs D
Xét tam giác ADEcó góc DEC là góc ngoài tại E
=> góc DEC=BAC+EDA
mà BAC> 90' (gt)
=>DEC>90 => DEC là góc tù
Xét tam giác DEC có DEC là góc tù
=>DC là cạnh lớn nhất trong tam giác ( đối diện vs góc tù)
=>DC>DE(1)
Từ (1),(2) ,=>DE<DC<BC
=>DE,BC (đpcm)
