Cho nữa đường tròn tâm O, đường kính AB = 2R . Vẽ các tiếp tuyến Ax và By với nửa đường tròn, từ một điểm M trên nửa đường tròn (M khác A và B) vẽ tiếp tuyến với nửa đường tròn và cắt Ax ; By theo thứ tự ở D và
. a) Chứng minh: Bốn điểm A, D, M, O cùng thuộc một đường tròn
b) Chứng minh: COD = 90 độ, AD. BC = R ^ 2
c) Gọi N là giao điểm của AC và BD; MN cắt AB tại H. Chứng minh N là trung điểm của MH.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

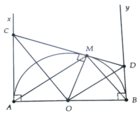
a, HS tự chứng minh
b, ΔCOD và ΔAMB đồng dạng => MC.MD = O M 2
c, AC = R 3
BD.AC = MC.MD = O M 2
=> BD = R 3 3

a: góc OAC+góc OMC=180 độ
=>OACM nội tiếp
b: góc BOM=2*60=120 độ
=>góc BDM=60 độ
=>ΔBMD đều
\(S_{qMB}=\dfrac{pi\cdot R^2\cdot120}{360}=\dfrac{1}{3}\cdot pi\cdot R^2\)

a: Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
=>ΔMAO=ΔMCO
=>góc MCO=90 độ
góc MAO+góc MCO=180 độ
=>MAOC nội tiếp đường tròn đường kính MO
=>I là trung điểm của MO
b: góc MCO=90 độ
=>MC là tiếp tuyến của (O)
Xét ΔMCD và ΔMBC có
góc MCD=góc MBC
góc CMD chung
=>ΔMCD đồng dạng với ΔMBC
=>MC/MB=MD/MC
=>MC^2=MB*MD

b: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=AC+BD

