Câu a,b không cần làm ,chỉ cần làm câu c,d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2021
Bài 4:
b) \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{4-7}=\dfrac{24}{-3}=-8\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).4=-12\\y=\left(-3\right).7=-28\end{matrix}\right.\)
c) Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{2x}{6}=\dfrac{3y}{12}=\dfrac{2x-3y}{6-12}=\dfrac{24}{-6}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).3=-12\\y=\left(-4\right).4=-16\end{matrix}\right.\)
3 tháng 10 2021
Bài 3:
a: Ta có: \(\dfrac{2.5}{7.5}=\dfrac{x}{\dfrac{3}{5}}\)
\(\Leftrightarrow\dfrac{x}{\dfrac{3}{5}}=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{5}\)
b: Ta có: \(\dfrac{5}{6}:x=\dfrac{20}{3}\)
\(\Leftrightarrow x=\dfrac{5}{6}:\dfrac{20}{3}=\dfrac{15}{120}=\dfrac{1}{8}\)
LN
1
3 tháng 10 2021
không cần làm bài 1 với cả câu d bài 4 đâu nhé các bạn
cảm ơn mọi người
7 tháng 12 2021
Câu b bạn tự vẽ
Câu c:
PT hoành độ giao điểm: \(-3x+1=\left(1-2m\right)x+m-1\)
Mà 2 đt cắt tại hoành độ 1 nên \(x=1\)
\(\Leftrightarrow-2=1-2m+m-1\Leftrightarrow m=2\)
Câu d:
PT giao Ox,Oy lần lượt tại A,B của (d) là:
\(\left\{{}\begin{matrix}y=0\Rightarrow x=\dfrac{m-1}{2m-1}\Rightarrow A\left(\dfrac{m-1}{2m-1};0\right)\Rightarrow OA=\left|\dfrac{m-1}{2m-1}\right|\\x=0\Rightarrow y=m-1\Rightarrow B\left(0;m-1\right)\Rightarrow OB=\left|m-1\right|\end{matrix}\right.\)
Gọi H là chân đường cao từ O đến (d)
Đặt \(OH^2=t\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m-1\right)^2}{\left(m-1\right)^2}+\dfrac{1}{\left(m-1\right)^2}\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{4m^2-4m+2}{\left(m-1\right)^2}\Leftrightarrow t=\dfrac{m^2-2m+1}{4m^2-4m+2}\\ \Leftrightarrow4m^2t-4mt+2t=m^2-2m+1\\ \Leftrightarrow m^2\left(4t-1\right)+2m\left(1-2t\right)+2t-1=0\)
Coi đây là PT bậc 2 ẩn m, PT có nghiệm
\(\Leftrightarrow\Delta'=\left(1-2t\right)^2-\left(4t-1\right)\left(2t-1\right)\ge0\\ \Leftrightarrow4t^2-4t+1-8t^2+6t-1\ge0\\ \Leftrightarrow2t-4t^2\ge0\\ \Leftrightarrow2t\left(1-2t\right)\ge0\\ \Leftrightarrow0\le t\le\dfrac{1}{2}\)
\(\Leftrightarrow OH^2\le\dfrac{1}{2}\Leftrightarrow OH\le\dfrac{1}{\sqrt{2}}\)
Dấu \("="\Leftrightarrow\dfrac{m^2-2m+1}{4m^2-4m+2}=\dfrac{1}{2}\Leftrightarrow4m^2-4m+2=2m^2-4m+2\)
\(\Leftrightarrow2m^2=0\Leftrightarrow m=0\)
Vậy m=0 thỏa yêu cầu đề
6 tháng 12 2021
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
SD
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
2
ML
7 tháng 3 2023
a/
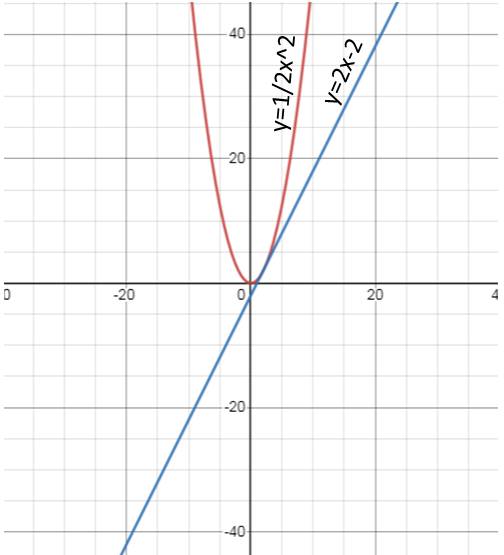
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
KV
7 tháng 3 2023
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)
VT
không cần làm hết đâu ạ chỉ cần 2,3 câu là đc ạ
1
28 tháng 10 2021
\(2,\Leftrightarrow\left\{{}\begin{matrix}20x+25y-10xy=0\\20x-30y+xy=0\end{matrix}\right.\Leftrightarrow55y-11xy=0\\ \Leftrightarrow11y\left(5-x\right)=0\Leftrightarrow\left[{}\begin{matrix}y=0\\x=5\end{matrix}\right.\)
Với \(y=0\Leftrightarrow4x+0=0\Leftrightarrow x=0\)
Với \(x=5\Leftrightarrow20+5y=10y\Leftrightarrow y=4\)
Vậy \(\left(x;y\right)=\left\{\left(0;0\right);\left(5;4\right)\right\}\)
TK
10 tháng 1 2020
c) tam c/m được t/g ABC cân tại A
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường trung tuyến nên DB=DC
t/g FDB=t/g EDC (cạnh huyền-góc nhọn)
=> DF=DE
d) có BF=EC (t/g FDB=t/g EDC)
và AB=AC (t/g ABC cân)
nên AB-BF=AC-EC
=> AF=AE
=> t/g AFE cân tại A
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường cao nên AD vuông góc với EF
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường cao nên AD vuông góc với BC (t/g ABC cân tại A)
ta có AD vuông góc với EF và BC nên EF//BC
