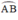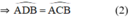Cho tam giác ABC nội tiếp đường tròn (O),
AB < AC. Tia phân giác của góc A cắt BC ở D, cắt
đường tròn ở E. Trên tia AC lấy điểm K sao cho AK
= AB. Chứng minh rằng:
a) ∆ABD = ∆AKD
b) DKCE là tứ giác nội tiếp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
27 tháng 5 2018
B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
HL
7 tháng 4 2015
câu d:
Tam giác BCF nội tiếp (O;BC/2) có cạnh BC là đường kính
=> Tam giác BCF vuông tại F
=>góc BFC=90 độ
Xét 2 tam giác: tam giác CHF và tam giác CFB có:
góc C chung
góc CHF=góc CFB (=90 độ)
Do đó, tam giác CHF đồng dạng với tam giác CFB (g.g)
=> góc CFH=góc CBF (1)
Tứ giác ABFC nội tiếp (O;BC/2)
=> góc CFH=góc ABC (cùng chắn cung AC) (2)
Từ (1) và (2)=> góc CBF=góc ABC (3)
Mà tia BC nằm giữa tia AB và BF (4)
Từ (3) và (4)=> BC là tia phận giác của góc ABF (đpcm)
30 tháng 6 2015
b)
+ Xét đt (o) có
tứ giác BFACN nội tiếp đt
\(\rightarrow ABC\)=AFC ( 2 góc nt cùng chắn cung AC)
CÓ :
BD là tiếp tuyến đt (o) tại B(gt)
\(\rightarrow\) BD vuông góc BO (TC tiếp tuyến)
\(\rightarrow\)BD vuông góc BC (O thuộc BC)
\(\rightarrow\) DBC = 90(dn)
\(\rightarrow\)tam giác DBC vuông tại B
xét tam giác vuông DBC cso
BDC+DCB=90(2 góc phụ nhau trong tg vuông) (1)
+Xét đt (o) có:
BAC= 90 ( góc nt chắn nửa dtđk BC)
\(\rightarrow\)tam giác BAC vuông tại A
Xét tam giác vuông BAC có
ABC+ACB=90 (2 gọc phụ nhau trong tam giác vuông)
\(\rightarrow\) ABC+DCB=90(A thuộc DC ) (2)
từ(1) và(2) \(\rightarrow\) BDC=ABC( cùng phụ DCB)
Mà AFC=ABC(CMT)
\(\rightarrow\) BDC=AFC(=ABC)
+Có :
AFC+AFE=180( 2 góc kề bù)
Mà 2 góc ở vị trí đối nhau
\(\rightarrow\) tứ giác DEFA nội tiếp ( DHNB tứ giác nội tiếp)
| |
CM
19 tháng 11 2019
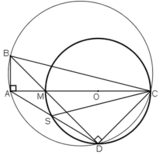
a)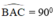 
⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
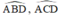đều là góc nội tiếp chắn cung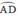 
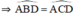
c) + Trong đường tròn đường kính MC:
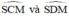đều là các góc nội tiếp cùng chắn cung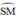 
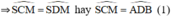
+ Trong đường tròn đường kính BC:
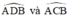đều là các góc nội tiếp chắn cung 
