Cho tam giác ABC có BA<BC.Trên tia BA lấy điểm D sao cho BD=BC.Tia phân giác của góc B cắt AC và DC lần lượt tại E và I
a,Chứng minh rằng : tam giác BEC=tam giác BED
b,Chứng minh ID=IC
c,Từ A kẻ AH vuông góc với DC tại H.Chứng minh AH//BI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 10 2019
Gọi D, E, F theo thứ tự là trung điểm của BC, CA, AB. Đường trung trực của BC phải vuông góc với EF (vì (EF // BC), hay nó là một đường cao của tam giác DEF. Suy ra ba đường trung trực của tam giác ABC là ba đường cao của tam giác DEF. Do đó tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực của tam giác ABC) là trực tâm của tam giác DEF.
21 tháng 3 2019
ta có: AB,AC,BC tỉ lệ với 3;4;5
\(\Rightarrow\frac{AB}{3}=\frac{AC}{4}=\frac{BC}{5}=\frac{AB+AC+BC}{3+4+5}=\frac{24}{12}=2.\)
=> AB = 6 (cm)
AC = 8 (cm)
BC = 10 (cm)
ta có: AB2 + AC2 = 82 + 62 = 100
BC2 = 102 = 100
=> AB2 + AC2 = BC2
=> tg ABC vuông tại A ( đlí py-ta-go đảo)
mà AB < AC
=> ^C < ^B <90 độ
^A = 90 độ
=> ^C < ^B < ^A
PT
1
CM
10 tháng 3 2017
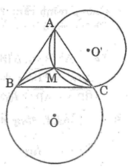
Vì M nằm trong tam giác ABC nên ta có:
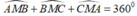
Khi đó điểm M nhìn các cạnh AB,BC,CA của tam giác ABC dưới một góc bằng 120 °
Ta có thẻ dựng điểm M như sau:
Dựng cung chứa góc 120 ° vẽ trên đoạn BC
Dựng cung chứa góc 120 ° vẽ trên đoạn AC
Giao điểm thứ hai ngoài C của hai cung này là điểm M cần dựng
CM
30 tháng 3 2017
a. Do BC > AC > AB ⇒ ∠A > ∠B > ∠C
Ta có AB2 + AC2 = 62 + 82 = 100 = 102 = BC2
Vậy tam giác ABC vuông tại A (1 điểm)
