Cho các số thực x, y thỏa mãn x2 + y2 = 1. Giá trị nhỏ nhất của S = x + y bằng:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=16\)
\(\Rightarrow x+y\ge-4\)
\(S_{min}=-4\)

Điểm rơi: \(x=y=\frac{\sqrt{2}}{2}\)
Ta tách biểu thức được như sau: \(A=x+\frac{1}{x}+y+\frac{1}{y}=(x+\frac{1}{2x})+(y+\frac{1}{2y})+\frac{1}{2}(\frac{1}{2x}+\frac{1}{2y})\)
\(\geq 2\sqrt{x.\frac{1}{2x}}+2\sqrt{y.\frac{1}{2y}}+\frac{1}{2}.\frac{4}{x+y}=2\sqrt{2}+\frac{2}{x+y}\)
Áp dụng bất đẳng thức Bunhiacốpxki, ta lại có:
\((x+y)^2\leq 2(x^2+y^2)=2 \Rightarrow x+y\leq \sqrt{2}\)
\(\Rightarrow A\geq 3\sqrt{2}\)
Dấu bằng xảy ra khi \(x=y=\frac{\sqrt{2}}{2}\)

Do \(x^2+y^2=1\), đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(P=\left(3-sina\right)\left(3-cosa\right)=9-3\left(sina+cosa\right)+sina.cosa\)
Đặt \(sina+cosa=t\Rightarrow t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(t^2=1+2sina.cosa\Rightarrow sina.cosa=\dfrac{t^2-1}{2}\)
\(P=9-3t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2-3t+\dfrac{17}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(f'\left(t\right)=t-3=0\Rightarrow t=3\notin\left[-\sqrt{2};\sqrt{2}\right]\)
\(f\left(-\sqrt{2}\right)=\dfrac{19+6\sqrt{2}}{2}\) ; \(f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\)
\(\Rightarrow P_{min}=f\left(\sqrt{2}\right)=\dfrac{19-6\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)
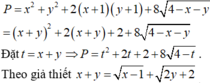
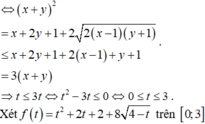
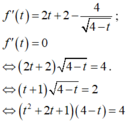
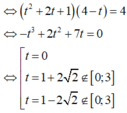




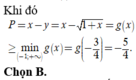
\(\left(x+y\right)^2\le2\left(x^2+y^2\right)=2\)
\(\Rightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(S_{min}=-\sqrt{2}\)