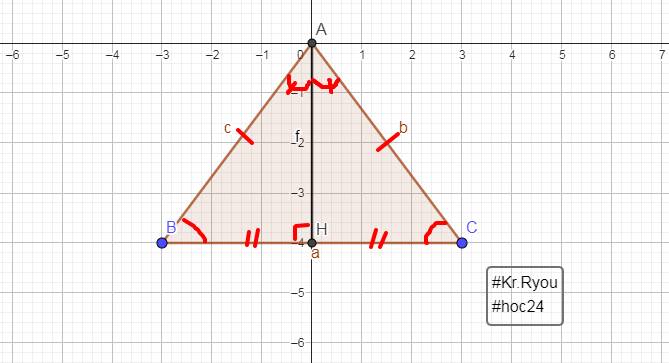
Cho tam giác ABC cân tại A có AH phân giác góc A cắt BC tại H . chứng minh
a. Tam giác AHB = tam giác AHC
b. BH = Hc
giúp em với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2022
a: Xét ΔHBA vuông tại H và ΔHCA vuông tại H có
AH chung
AB=AC
Do đó: ΔHBA=ΔHCA
b: Xét ΔABM và ΔACM có
AB=AC
góc BAM=góc CAM
AM chung
Do đó: ΔABM=ΔACM
=>góc MAB=góc MAC
c: ΔABM=ΔACM
nên MB=MC
26 tháng 6 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: Xét ΔDMH vuông tại M và ΔDMC vuông tại M có
DM chung
MH=MC
=>ΔDMH=ΔDMC
=>góc DHC=góc DCH
=>góc DHC=góc ABH
=>DH//AB
c: Xét ΔAHC có
M là trung điểm của CH
MD//AH
=>D là trung điểm của AC
Xét ΔABC có
BD,AH là đường cao
BD cắt AH tại G
=>G là trọng tâm
7 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC,}` $\widehat {B} = \widehat {C}$
Vì `\text {AH}` là đường cao
`-> \text {AH} \bot \text {BC}`
`->` $\widehat {AHB} = \widehat {AHC} = 90^0$
Xét `2 \Delta` vuông `AHB` và `AHC`:
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`-> \text {HB = HC (2 cạnh tương ứng)}`
`-> \text {H là trung điểm của BC}`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường trung tuyến}`
`-> \text {H là trung điểm của BC}`
`c,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
`-> \text {AH là tia phân giác của} \Delta ABC`
Hoặc bạn có thể dùng cách này (nếu đã học về tính chất của `\Delta` cân đối với các đường trong `\Delta`)
Vì `\Delta ABC` cân tại A.
Mà `\text {AH}` là đường cao
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {AH cũng là đường phân giác}`
7 tháng 6 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
20 tháng 1 2022
Vì AH là đường phân giác mà tam giác ABC cân tại A
=> AH là đường trung tuyến => BH = HC
Xét tam giác AHB và tam giác AHC có :
AH _ chung
BH = HC ( cmt )
AB = AC
Vậy tam giác AHB = tam giác AHC ( c.c.c )
Vì AH là đường trung tuyến => BH = BC/2 = 3 cm
và
20 tháng 1 2022
nãy mình ấn lộn bạn thông cảm mình nhé
và AH cũng đồng thời là đường cao
Xét tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+BH^2}=\sqrt{16+9}=5cm\)
=> BA = AC = 5 cm ( do tam giác ABC cân tại A )
12 tháng 3 2022
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm
8 tháng 4 2022
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAHM=ΔAHN
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Ta có: AM=AN
HM=HN
Do đó: AH là đường trung trực của MN
hay AH⊥MN
TC
8 tháng 4 2022
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
cạnh AH chung
AB=AC(vì tam giác ABC cân tại A)
=> ΔAHB=ΔAHC(c.h-c.g.v)
Xét ΔAHM vuông tại M và ΔAHN vuông tại N có
\(\widehat{HAM}=\widehat{HAN}\)
cạnh AH chung
==> ΔAHM=ΔAHN(c.h-g.n)
==> AM=AN
=> ΔAMN cân tại A ( dấu hiệu)
c)Ta có:HM=HN ; AM=AN
===>AH là đường trung trực của MN
=>\(\text{AH⊥MN}\)
a.Ta có : tam giác ABC cân tại A
=>AB=AC;B=C
Xét tam giác AHB và tam giác AHC ta có:
B=C(gt)
AB=AC(gt)
BAH=HAC( p/g)
=>tam giác AHB=tam giác AHC(g-c-g)(dpcm)
b.Theo câu a ta có:
BH=HC (2 cạnh tương ứng)(dpcm)