Question

[20_Trần Thị Trà My]

Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi I, J lần lượt là trung điểm của BC, SC, và K là điểm trên SD sao cho SK = 1/2 KD . a) Chứng minh rằng OJ / /(SAC) và OJ / /(SAB). b) Chứng minh rằng OI / /(SCD) và IJ / /(SBD). c) Gọi M là giao điểm của AI và BD. Chứng minh rằng MK / /(SBC). Cần gấp ạhh

Answer 1

[Nguyễn Việt Lâm]

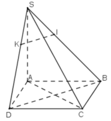
a.

Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC

\(\Rightarrow OJ\) là đường trung bình tam giác SAC

\(\Rightarrow OJ||SA\)

Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)

\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)

b. O là trung điểm BD, I là trung điểm BC

\(\Rightarrow OI\) là đườngt rung bình tam giác BCD

\(\Rightarrow OI||CD\)

Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)

Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)

c. Ta có I là trung điểm BC, O là trung điểm AC

\(\Rightarrow M\) là trọng tâm tam giác ABC

\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\) 

\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)

Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)

\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)

\(\Rightarrow MK||\left(SBC\right)\)

Answer 2

[Nguyễn Việt Lâm]