Giải hệ phương trình 2x+3y=7 và 4x-y=7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2016
ta có 2x+3y=7(1) => 4x+6y=14( nhân đôi 2 vế)
=> 4x+6y-(4x-y)=14-7
=> 4x+6y-4x+y=7
=> 6y+y=7
=> 7y=7 =>y=1
thay vào (1) ta có 2x+3.1=7 =>2x=4 => x=2
chúc bạn học tốt. ủng hộ mik nha
5 tháng 10 2021
a: Ta có: \(\left\{{}\begin{matrix}2x-10y=-7\\10x+11y=31\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10x-50y=-35\\10x+10y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-60y=-66\\2x-10y=-7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{11}{10}\\2x=-7+10y=-7+11=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{11}{10}\end{matrix}\right.\)
CM
19 tháng 2 2019
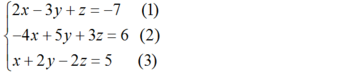
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
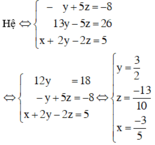
Vậy hệ phương trình có nghiệm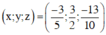 
NT
4 tháng 4 2016
(1)=>2x=4-IyI
thay vô (2) ta dc (4-IyI)*2-3y=1
ta có 2 trường hợp
- (4-y)*2-3y=1
- (4+y)*2-3y=1
RN
0
28 tháng 9 2021
h) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=2\\\dfrac{3}{x}-\dfrac{4}{y}=-1\end{matrix}\right.\)\(\left(1\right)\)\(\left(đk:x,y\ne0\right)\)
Đặt \(a=\dfrac{1}{x},b=\dfrac{1}{y}\)
\(\left(1\right)\Leftrightarrow\) \(\left\{{}\begin{matrix}a+b=2\\3a-4b=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3a+3b=6\\3a-4b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=2\\7b=7\end{matrix}\right.\)\(\Leftrightarrow a=b=1\)
Thay a,b:
\(\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{y}=1\Leftrightarrow x=y=1\left(tm\right)\)
CM
7 tháng 11 2019
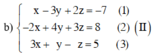
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với (3) rồi trừ đi phương trình (3) ta được:
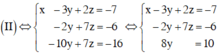
Giải hệ phương trình trên ta được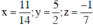 
Vậy hệ phương trình có nghiệm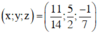 
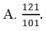
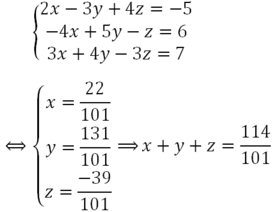
ta có 2x+3y=7(1) => 4x+6y=14( nhân đôi 2 vế)
=> 4x+6y-(4x-y)=14-7
=> 4x+6y-4x+y=7
=> 6y+y=7
=> 7y=7 =>y=1
thay vào (1) ta có 2x+3.1=7 =>2x=4 => x=2
chúc bạn học tốt. ủng hộ mik nha