Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm A( 2;1), B(4;0), C(2; 3).
a) Tìm tọa độ trọng tâm G của tam giác ABC và trung điểm I của cạnh AB.
b) Cho D (m ; 2). Tìm m để ba điểm A, B, D thẳng hàng.
c) Tính cos của góc B trong tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(-4;4\right)=-4\left(1;-1\right)\)
\(\Rightarrow\) Phương trình CD song song AB đi qua D có dạng:
\(1\left(x+6\right)+1\left(y+8\right)=0\Leftrightarrow x+y+14=0\)
Gọi M là trung điểm AB \(\Rightarrow M\left(-6;4\right)\)
Phương trình đường thẳng d qua M và vuông góc AB có dạng:
\(1\left(x+6\right)-1\left(y-4\right)=0\Leftrightarrow x-y+10=0\)
Gọi N là giao điểm CD và d \(\Rightarrow\) N là trung điểm CD do ABCD là hình thang cân
Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x+y+14=0\\x-y+10=0\end{matrix}\right.\) \(\Rightarrow N\left(-12;-2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_C=2x_N-x_D=...\\y_C=2y_N-y_D=...\end{matrix}\right.\)

\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)=\left(3;-9\right)\)

\(AB=\sqrt{\left(3-1\right)^2+\left(4-2\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(6-1\right)^2+\left(-5-2\right)^2}=\sqrt{74}\)
\(BC=\sqrt{\left(6-3\right)^2+\left(-5-4\right)^2}=3\sqrt{10}\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{-\sqrt{37}}{37}\)
=>góc A=99 độ
AB/sinC=AC/sinB=BC/sinA
=>\(\dfrac{3\sqrt{10}}{sin99}=\dfrac{2\sqrt{2}}{sinC}=\dfrac{\sqrt{74}}{sinB}\)
=>góc C=17 độ; góc B=64 độ

Giả sử tọa độ M(x;0). Khi đó \(\overrightarrow{MA}=\left(1-x;2\right);\overrightarrow{MB}=\left(4-x;3\right)\)
Theo giả thiết ta có \(\overrightarrow{MA}.\overrightarrow{MB}=MA.MB.\cos45^0\)
\(\Leftrightarrow\left(1-x\right)\left(4-x\right)+6=\sqrt{\left(1-x\right)^2+4}.\sqrt{\left(4-x\right)^2+9}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow x^2-5x+10=\sqrt{x^2-2x+5}.\sqrt{x^2-8x+25}.\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow2\left(x^2-5x+10\right)^2=\left(x^2-5x+10\right)\left(x^2-8x+25\right)\) (do \(x^2-5x+10>0\))
\(\Leftrightarrow x^4-10x^3+44x^2-110x+75=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-5\right)\left(x^2-4x+15\right)=0\)
\(\Leftrightarrow x=1;x=5\)
Vậy ta có 2 điểm cần tìm là M(1;0) hoặc M(5;0)

![]()
Suy ra mặt phẳng (ABC) có một VTPT là ![]()
Mặt phẳng (Oxy) có một VTPT là k → = 0 ; 0 ; 1
Gọi φ là góc giữa hai mặt phẳng (ABC) và (Oxy). Ta có
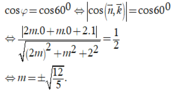
Chọn C.

Đáp án B
Phương pháp :
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c>0) => OA = a; OB = b; OC = c
Viết phương trình mặt phẳng (P): x a + y b + z c = 1
Cách giải :
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c>0) => OA = a; OB = b; OC = c
O
A
1
=
O
B
2
=
O
C
4
<=> 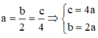
Khi đó phương trình mặt phẳng (P) là: x a + y 2 a + z 4 a = 1
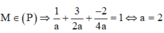
Vậy phương trình mặt phẳng (P) là :
x 2 + y 4 + z 8 = 1 <=> 4x + 2y + z – 8 = 0

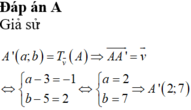
a: \(\left\{{}\begin{matrix}x_G=\dfrac{2+4+2}{3}=\dfrac{8}{3}\\y_G=\dfrac{1+0+3}{3}=\dfrac{4}{3}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_I=\dfrac{2+4}{2}=3\\y_I=\dfrac{1+0}{2}=\dfrac{1}{2}\end{matrix}\right.\)