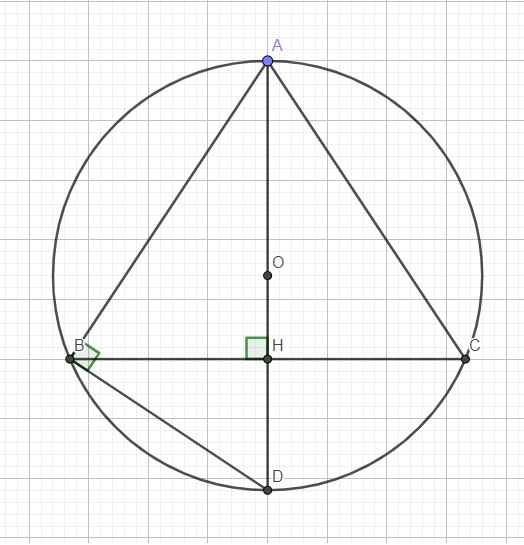
Cho tam giác ABC vuông cân tại A, đường cao AH. Biết AB = 5cm, BC = 6cm. a/ Tính các góc và các cạnh còn lại của tam giác ABC. b/ Dựng đường tròn tâm (O) ngoại tiếp tam giác ABC, tính độ dài bán kính của đường tròn tâm O.![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẽ OA cắt đường tròn tại D cắt BC tại K
Ta có OA = OB = OD = R
\(\Rightarrow\)\(\Delta ABD\) vuông tại D
\(\Rightarrow BD=\sqrt{OD^2-AB^2}=\sqrt{10^2-8^2}=6\)
Ta có OK là đường trung trực của BC nên \(\hept{\begin{cases}OK⊥BC\\BK=CK\end{cases}}\)
Ta lại có: \(S_{\Delta ABD}=\frac{1}{2}AB.BD=\frac{1}{2}AD.BK\)
\(\Rightarrow BK=\frac{AB.BD}{AD}=\frac{8.6}{10}=4,8\)
\(\Rightarrow BC=2BK=4,8.2=9,6\)
Viết nhầm tùm lum hết. Do không thấy cái hình. Mà thôi nhìn hình sửa hộ luôn nhé

bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ

Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung trực của BC
Mà tâm của đường tròn ngoại tiếp là giao của 3 đường trung trực hay tâm O nằm trên 3 đường trung trực
\(\Rightarrow O\in AH\)
Do AD là đường kính \(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ABD\) vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=7,2\left(cm\right)\)


c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c