Mặt phẳng nghiêng AB hợp với phương ngang một góc α = 300, như hình vẽ. Một vật có khối lượng m = 500 g, bắt đầu trượt không ma sát từ đỉnh A của mặt phẳng nghiêng có chiều dài AB = 2 (m) và sau đó tiếp tục trượt trên mặt phẳng nằm ngang một khoảng là BC. Lấy g = 10 m/s2.a. Tính cơ năng của vật tại A và B?b. Tính vận tốc của vật tại B?c. Tính độ dài đoạn BC, biết hệ số ma sát giữa vật với mặt...
Đọc tiếp
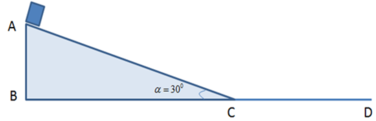
Mặt phẳng nghiêng AB hợp với phương ngang một góc α = 300, như hình vẽ. Một vật có khối lượng m = 500 g, bắt đầu trượt không ma sát từ đỉnh A của mặt phẳng nghiêng có chiều dài AB = 2 (m) và sau đó tiếp tục trượt trên mặt phẳng nằm ngang một khoảng là BC. Lấy g = 10 m/s2.
a. Tính cơ năng của vật tại A và B?
b. Tính vận tốc của vật tại B?
c. Tính độ dài đoạn BC, biết hệ số ma sát giữa vật với mặt phẳng ngang µ = 0,1
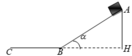
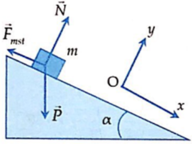
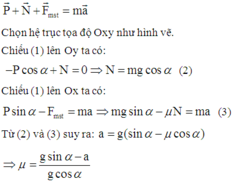
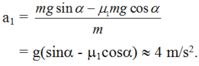
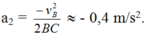
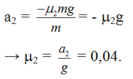
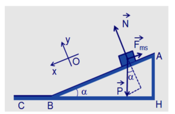
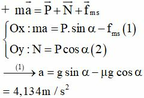
a) Chọn mốc thế năng tại chân mặt phẳng nghiêng
Ta có: \(h=l.\sin\alpha=\dfrac{1}{2}.2=1\left(m\right)\)
Cơ năng tại A \(W_A=\dfrac{1}{2}mv_A^2+mgz_A=0+mgz_A=5\left(J\right)\)
Bỏ qua ma sát trên mặt phẳng nghiêng cơ năng của vật được bảo toàn: \(W_A=W_B=5\left(J\right)\)
b) Bảo toàn cơ năng: \(W_A=W_B\Leftrightarrow mgz_A=\dfrac{1}{2}mv_B^2\Leftrightarrow v_B=\sqrt{2gz_A}=2\sqrt{5}\left(m/s\right)\)
c) Ta có: \(-F_{ms}=ma\Rightarrow-\mu mg=ma\Rightarrow a=-1\left(m/s^2\right)\)
\(v_C^2-v_B^2=2aS\Rightarrow S=10\left(m\right)\)