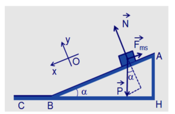
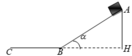
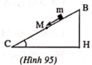
Một mặt phẳng AB nghiêng một góc a = 30o với mặt phẳng nằm ngang và dài AB = 1m. Mặt phẳng ngang BC = 10,35m. Một vật có khối lượng 1kg trượt không vận tốc ban đầu từ đỉnh A tới C thì dừng lại. Biết hệ số ma sát giữa vật và mặt phẳng nghiêng μ1 = 0,1 , lấy g = 10m/s. Tính:
a. Vận tốc của vật tại B.
b. Hệ số ma sát giữa vật và mặt phẳng ngang μ.
Ai chỉ giúp mình bài này với ạ!

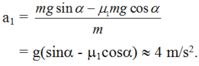
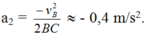
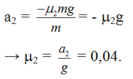
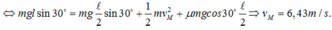
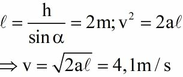
Định luật II Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Ox: \(Psin\alpha-F_{ms}=m\cdot a\)
Oy: \(N-Pcos\alpha=0\Rightarrow N=Pcos\alpha=mgcos\alpha\)
\(F_{ms}=\mu_1\cdot N=\mu_1\cdot mgcos\alpha\)
Gia tốc mặt phẳng nghiêng:
\(a=\dfrac{Psin\alpha-F_{ms}}{m}=\dfrac{mgsin\alpha-\mu_1mgcos\alpha}{m}=g\left(sin\alpha-\mu_1cos\alpha\right)=10\left(sin30-0,1cos30\right)\approx4,13\)m/s2