Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, xét tma giác AEB và tam giác DEC có :
BE = EC do E là trđ của BC (Gt)
AE = ED do E là trđ của AD (gt)
góc BEA = góc DEC (đối đỉnh)
=> tam giác AEB = tam giác DEC (c-g-c)
b, xét tam giác CEA và tam giác BED có:
BE = EC (Câu a)
AE = ED (câu a)
góc BED = góc CEA (đối đỉnh)
=> tam giác CEA = tam giác BED (c-g-c)
=> góc DBE = góc ECA (đn) mà 2 góc này slt
=> CA // BD (Đl)
c, xét tam giác AHC và tam giác KHC có : HC chung
AH = HK do K là trđ của AH (gt)
góc AHC = góc KHC =90
=> tam giác AHC = tam giác KHC (2cgv)
=> AC = CK (đn)
mà AC = BD do tam giác BED = tam giác CEA (Câu b)
=> BD = AC = CK
a: Xét ΔACH vuông tại H và ΔKCH vuông tại H có
HC chung
HA=HK
Do đó: ΔACH=ΔKCH
hình bạn nhé :
Xét ΔABEΔABE và ΔDCEΔDCE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEB=∠DEC∠AEB=∠DEC (đối đỉnh)
⇒ΔABE=ΔDCE(c−g−c)⇒ΔABE=ΔDCE(c−g−c)
b) Chứng minh: AC//BDAC//BD.
Xét ΔACEΔACE và ΔDBEΔDBE có :
EB=ECEB=EC (EE là trung điểm BCBC)
EA=EDEA=ED (EE là trung điểm ADAD)
∠AEC=∠DEB∠AEC=∠DEB (đối đỉnh)
⇒ΔACE=ΔDBE(c−g−c)⇒ΔACE=ΔDBE(c−g−c)
⇒∠ACE=DBE⇒∠ACE=DBE (góc tương ứng)
Mà hai góc ở vị trí so le trong nên AC//BDAC//BD (đpcm)
c) Vẽ AHAH vuông góc với ECEC (HH thuộc BCBC). Trên tia AHAH lấy điểm KK sao cho HH là trung điểm của AKAK. Chứng minh rằng BD=AC=CKBD=AC=CK.
Ta có : ΔACE=ΔDBE(cmt)ΔACE=ΔDBE(cmt)⇒BD=AC⇒BD=AC (cạnh tương ứng) (1)
Xét ΔCAHΔCAH và ΔCKHΔCKH có :
CHCH chung
∠CHA=∠CHK=900∠CHA=∠CHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔCAH=ΔCKH(c−g−c)⇒ΔCAH=ΔCKH(c−g−c)
⇒CA=CK⇒CA=CK (2)
Từ (1) và (2) suy ra AC=BD=CKAC=BD=CK (đpcm)
d) Chứng minh DKDK vuông góc với AHAH.
Nối EE với KK.
Xét ΔEAHΔEAH và ΔEKHΔEKH có :
EHEH chung
∠EHA=∠EHK=900∠EHA=∠EHK=900
HA=HK(gt)HA=HK(gt)
⇒ΔEAH=ΔEKH(c−g−c)⇒ΔEAH=ΔEKH(c−g−c) ⇒∠EAH=∠EKH⇒∠EAH=∠EKH (góc t/ư) (3)
EK=EAEK=EA (cạnh t/ư), mà EA=ED(gt)EA=ED(gt) ⇒EK=ED⇒EK=ED ⇒ΔEKD⇒ΔEKD cân tại EE
⇒∠EKD=∠EDK⇒∠EKD=∠EDK (t/c) (4)
Từ (3) và (4) suy ra ∠EAK+∠EDK=∠EKA+∠EKD=∠AKD∠EAK+∠EDK=∠EKA+∠EKD=∠AKD
Tam giác AKDAKD có : ∠EAK+∠EDK+∠AKD=1800∠EAK+∠EDK+∠AKD=1800
⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900⇒∠AKD+∠AKD=1800⇒2∠AKD=1800⇒∠AKD=1800:2=900
Vậy AK⊥KDAK⊥KD (đpcm).
chúc bạn học tốt
a: Xét ΔACH vuông tại H và ΔKCH vuông tại H có
HA=HK
HC chung
Do đó: ΔACH=ΔKCH
a: Xét ΔAIC và ΔDIB có
IA=ID
ˆAIC=ˆDIBAIC^=DIB^
IC=IB
Do đó: ΔAIC=ΔDIB
Suy ra: ˆACI=ˆDBIACI^=DBI^
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
a: Xét ΔAIC và ΔDIB có
IA=ID
\(\widehat{AIC}=\widehat{DIB}\)
IC=IB
Do đó: ΔAIC=ΔDIB
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AC//BD
c: Ta có: AH⊥BC
DK⊥BC
Do đó: AH//DK
Xét ΔAHI vuông tại H và ΔDKI vuông tại K có
IA=ID
\(\widehat{AIH}=\widehat{DIK}\)
Do đó: ΔAHI=ΔDKI
Suy ra; AH=DK
a, xét tam giác ACH và tam giác KCH có : CH chung
góc AHC = góc KHC = 90
AH = HK do H là trđ của AK (gt)
=> tam giác ACH = tam giác KCH (2cgv)
b, xét tam giác AEC và tam giác DEB có : góc BED = góc CEA (đối đỉnh)
BE= EC do E là trđ của BC (GT)
AE = ED do E là trđ của AD (gt)
=> tam giác AEC = tam giác DEB (c-g-c)
=> BD = AC (đn)
tam giác ACH = tam giác KCH (câu a) => AC = CK (đn)
=> BD = CK (tcbc)
c, xét tam giác AEH và tam giác KEH có: EH chung
AH = HK (câu a)
góc AHE = góc KHE = 90
=> tam giác AEH = tam giác KEH (2cgv)
=> góc AEH = góc KEH mà EH nằm giữa EA và EK
=> EH là phân giác của góc AEK (đn)
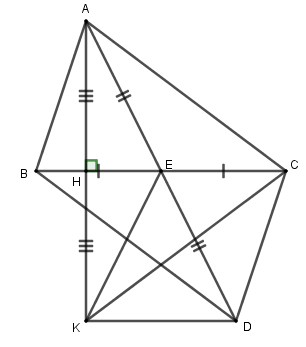
a) Xét ∆ABE và ∆DCE có:
+ ^AEB = ^DEC (2 góc đối đỉnh).
+ EB = EC (do E là trung điểm của BC).
+ EA = ED (do E là trung điểm của AD).
=> ∆ABE = ∆DCE (c - g - c).
b) Xét tứ giác ACDB có:
+ E là trung điểm của BC (gt).
+ E là trung điểm của AD (gt).
=> Tứ giác ACDB là hình bình hành (dhnb).
=> AC // BD (Tính chất hình bình hành).
c) Vì tứ giác ACDB là hình bình hành (cmt).
=> AC = BD (Tính chất hình bình hành). (1)
Xét tam giác ACK có:
+ CH là đường cao (do CH ⏊ AK).
+ CH là đường trung tuyến (do H là trung điểm của AK).
=> Tam giác ACK cân tại C.
=> AC = CK (Tính chất tam giác cân). (2)
Từ (1) và (2) => BD = AC = CK (đpcm).
d) Xét tam giác AKD có:
+ H là trung điểm của AK (gt).
+ E là trung điểm của AD (gt)
=> HE là đường trung bình.
=> HE // DK (Tính chất đường trung bình trong tam giác).
Mà HE ⏊ AH (do BC ⏊ AH).
=> DK ⏊ AH (Từ ⏊ đến //).