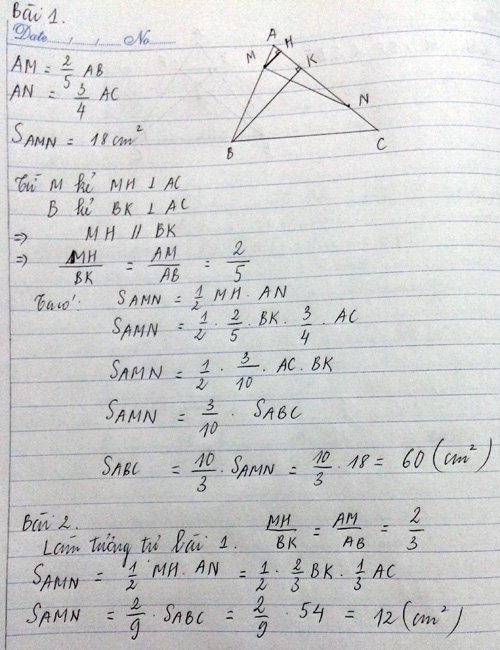Cho hình tam giác ABC có diện tích 36 cm vuông. Trên cạnh AB lấy 1 điểm M sao cho AM bằng 1/3 AB. Trên cạnh AC lấy điểm N sao cho AN bằng 1/3 AC. Tính diện tích AMN?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 6 2023
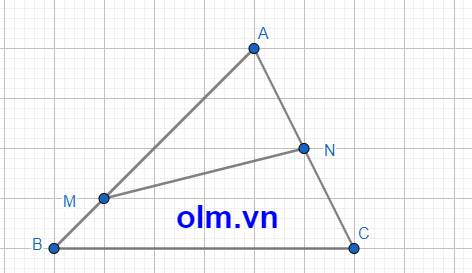
SAMN = \(\dfrac{1}{2}\) SAMC (vì hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy AC và AN = \(\dfrac{1}{2}\)AC)
SAMC = \(\dfrac{3}{4}\) SABC (vì hai tam giác có chung đường cao hạ từ đỉnh C xuống đáy AB và (AM = \(\dfrac{3}{4}\) AB)
⇒SAMN = SABC \(\times\) \(\dfrac{3}{4}\) \(\times\) \(\dfrac{1}{2}\) = \(\dfrac{3}{8}\) \(\times\) SABC
SABC = 48 : \(\dfrac{3}{8}\) = 128 (cm2)
Kết luận diện tích tam giác ABC là 128 cm2
VD
2 tháng 8 2018
Vì gấp rưỡi là gấp 3/2 còn 1 nửa là 1/2. Ta lấy 3/2 : 1/2 = 3.
Diện tích tam giác ABC là: 36 x 3 = 108
Diện tích tứ giác BMNC là: 108 - 36 = 72 (cm2)
Đ/s: 72 cm2
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
12 tháng 3 2023
a) ta thấy tỉ số diện tích tam giác ANB/ABC=1/3
tỉ số diện tích tam giác AMN/ANB=1/3 ( có chung chiều cao hạ từ N)
diện tích tam giác AMN là:
b) C với D như hình vẽ
ta thấy diện tích hai tam giác NDE bằng diện tích tam giác NDC ( có chung chiều cao và đáy )
từ đó suy ra:
vậy AND/NDE=1/2
