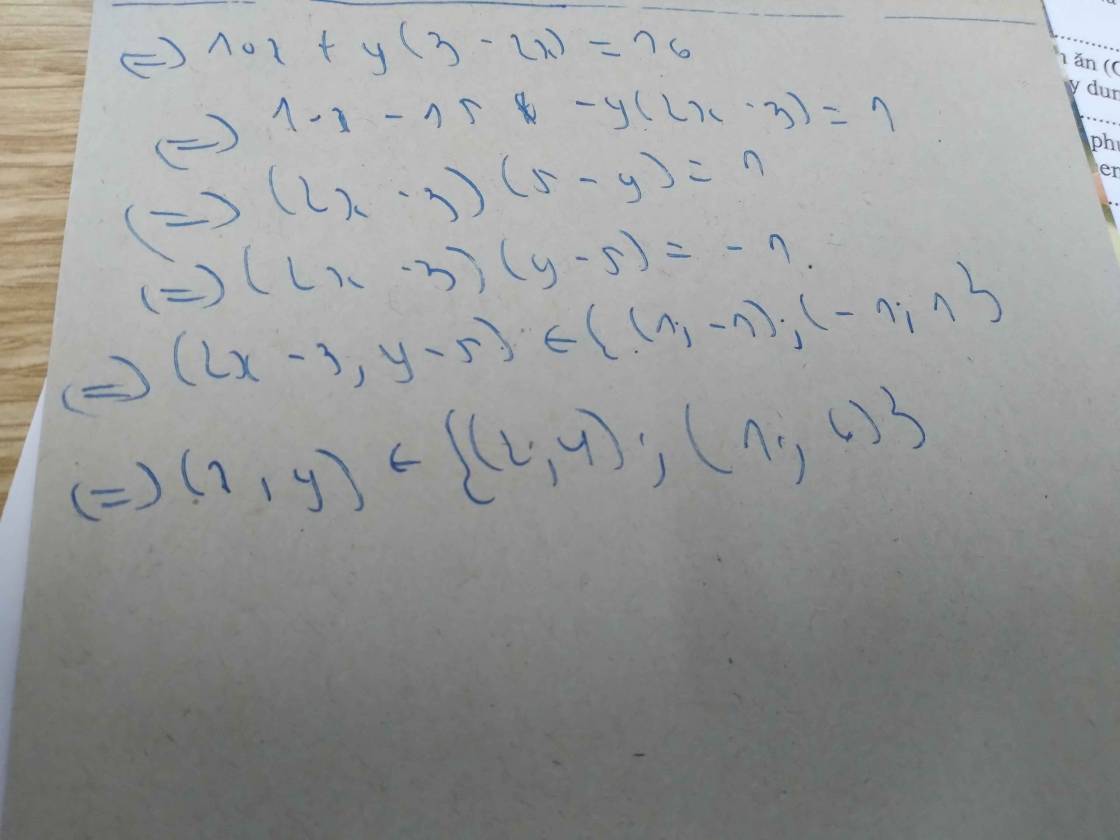Tìm x,y là số nguyên biết 6xy-10x-3y-4=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



=>3y(2x+1)-10x-5=7
=>(2x+1)(3y-5)=7
=>\(\left(2x+1;3y-5\right)\in\left\{\left(1;7\right);\left(7;1\right)\right\}\)(Vì x,y là số nguyên)
=>\(\left(x,y\right)\in\left\{\left(0;6\right);\left(3;2\right)\right\}\)

`9x2 + 3y2 + 6xy - 6x + 2y - 35 = 0`
`<=> (9x2 + 6xy + y2) - 2(3x + y) + 1 + 2(y2 + 2y + 1) - 37 = 0`
`<=> (3x + y - 1)2 = 37 - 2(y + 1)^2`
Vì `(3x+y=1)^2>=0`
`=>2(y+1)^2<=37`
`=>(y+1)^2<=37/2`
Mà `(y+1)^2` là scp
`=>(y+1)^2 in {0,1,4,8,16}`
`=> y + 1 ∈{0; 1; -1; 2; -2; 3; -3; 4; -4}`
`=>y in {-1,0,-2,1,-3,2,-4,3,-5}`
Đến đây dễ rồi thay y vào rồi tìm x thôi!

6xy-3y-4x=4
3y.(2x-1)-2.(2x-1)=6
(2x-1).(3y-2)=6
vì x,y là số nguyên nên ta có : x=-1,y=3


6xy+4x-3y=8
=> 6xy -3y=8-4x
=>3y(2x-1)= -2(2x-1) +6
=>(2x-1)(3y+2)=6
mà x,y thuộc Z =>(2x-1),(3y+2) thuộc Z =>(2x-1),(3y+2) thuộc U(6) xong giải ra bình thường nhé mấy câu sau tương tự

9x2 + 3y2 + 6xy - 6x + 2y - 35 = 0
<=> (9x2 + 6xy + y2) - 2(3x + y) + 1 + 2(y2 + 2y + 1) - 37 = 0
<=> (3x + y - 1)2 = 37 - 2(y + 1)2
Ta có: (3x + y - 1)2 \(\ge\)0 => 37 - 2(y + 1)2 \(\ge\)0
=> (y + 1)2 \(\le\)37/2
Do y nguyên và (y + 1)2 là số chính phương
=> (y + 1)2 \(\in\){0; 1; 4; 9; 16}
=> y + 1 \(\in\){0; 1; -1; 2; -2; 3; -3; 4; -4}
Lập bảng
| y + 1 | 0 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 |
| y | -1 | 0 | -2 | 1 | -3 | 2 | -4 | 3 | -5 |
Với y = -1 => (3x - 1 - 1)2 = 37 - 2(-1 + 1)2
<=> (3x - 2)2 = 37
Do x nguyên và (3x - 2)2 là số chính phương
mà 37 là số nguyên tố => ko có giá trị y tm
.... (tự thay y vào)
bài trc sai