Giúp em bài 8 và 9 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
a: Ta có: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Thay \(x=11-6\sqrt{2}\) vào M, ta được:
\(M=\dfrac{3-\sqrt{2}+1}{3-\sqrt{2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=-2\sqrt{2}+1\)
Bài 8:
a) \(M=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{11-6\sqrt{2}}+1}{\sqrt{11-6\sqrt{2}}-3}=\dfrac{\sqrt{\left(3-\sqrt{2}\right)^2}+1}{\sqrt{\left(3-\sqrt{2}\right)^2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=1-2\sqrt{2}\)
c) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=3\)
\(\Leftrightarrow3\sqrt{x}-9=\sqrt{x}+1\Leftrightarrow2\sqrt{x}=10\Leftrightarrow\sqrt{x}=5\Leftrightarrow x=25\left(tm\right)\)
d) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}< 1\)
\(\Leftrightarrow\sqrt{x}+1< \sqrt{x}-3\Leftrightarrow1< -3\left(VLý\right)\)
Vậy \(S=\varnothing\)
e) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\in Z\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{1;16;25;49\right\}\)

Bài 8:
a) \(A=\dfrac{\sqrt{a}-1}{\sqrt{a}}.\dfrac{\sqrt{a}+1+\sqrt{a}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\)
b) \(A=\dfrac{2}{\sqrt{a}+1}=\dfrac{2}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{2}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{2}{\sqrt{2}-1+1}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Bài 9:
\(pt\Leftrightarrow\sqrt{\left(3x+1\right)^2}=2\)\(\Leftrightarrow\left|3x+1\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=2\\3x+1=-2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}3x=1\\3x=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-1\end{matrix}\right.\)

8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số

8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)

Bài 7:
Ta có: \(n_{Na_2O}=\dfrac{6,2}{62}=0,1\left(mol\right)\)
\(n_{H_2O}=\dfrac{73,8}{18}=4,1\left(mol\right)\)
PT: \(Na_2O+H_2O\rightarrow2NaOH\)
Xét tỉ lệ: \(\dfrac{0,1}{1}< \dfrac{4,1}{1}\), ta được H2O dư.
Theo PT: \(n_{NaOH}=2n_{Na_2O}=0,2\left(mol\right)\)
Ta có: m dd sau pư = mNa2O + mH2O = 6,2 + 73,8 = 80 (g)
\(\Rightarrow C\%_{NaOH}=\dfrac{0,2.40}{80}.100\%=10\%\)
Bạn tham khảo nhé!
Bài 8:
Ta có: \(n_{Zn}=\dfrac{6,5}{65}=0,1\left(mol\right)\)
PT: \(Zn+2HCl\rightarrow ZnCl_2+H_2\)
____0,1____0,2__________0,1 (mol)
a, VH2 = 0,1.22,4 = 2,24 (l)
b, \(C_{M_{HCl}}=\dfrac{0,2}{0,1}=2M\)
Bạn tham khảo nhé!

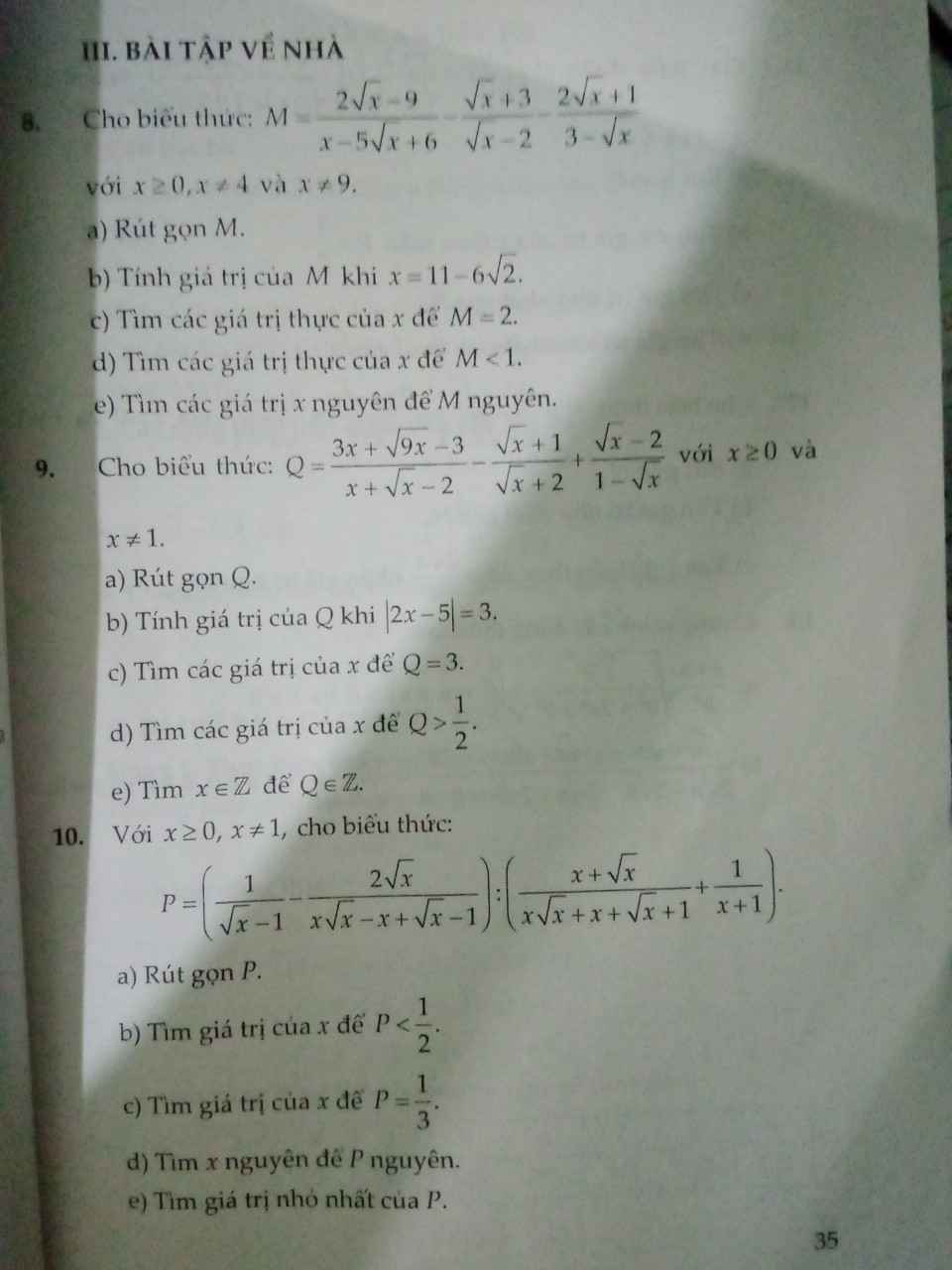
 giúp em bài 8 với 9 ạ :<
giúp em bài 8 với 9 ạ :<




 m.n ơi giúp em giải câu 8 và 9 với ạ. em sắp thi rồi
m.n ơi giúp em giải câu 8 và 9 với ạ. em sắp thi rồi
Bài 10:
a: =254-254+135=135