cho tam giác abc vuông tại a gọi m,n lần lượt là trung điểm của các cạnh bc và ac gọi e là điểm đối xứng với m qua ab chứng minh aebm là hình thoi
<cho xin , mình cần gấp> xin cảm ơn trước
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 11 2021
Xét tứ giác AEBM có
Hai đường chéo AB và EM cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau
nên AEBM là hình thoi
25 tháng 12 2021
a: Xét tứ giác AMBN có
Q là trung điểm của AB
Q là trung điểm của MN
Do đó: AMBN là hình bình hành
mà MA=MB
nên AMBN là hình thoi
CM
4 tháng 1 2020
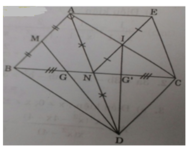
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
8 tháng 1 2022
1: BC=5cm
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình
=>DM=AC/2=2(cm)
2: Xét tứ giác ACME có
ME//AC
ME=AC
Do đó: ACME là hình bình hành
Xét tứ giác AEBM có
D là trung điểm của ME
D là trung điểm của AB
Do đó: AEBM là hình bình hành
mà MA=MB
nên AEBM là hình thoi
Xét tứ giác AEBM có
Hai đường chéo AB và EM cắt nhau tại trung điểm của mỗi đường và vuông góc với nhau
nên AEBM là hình thoi