D = 12 + 22 + 32 + .... +...
Đọc tiếp
D = 12 + 22 + 32 + .... + n2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 11 2021
TK
S=1.4+2.5+3.6+4.7+....+n.(n+3) S = 1. ( 2 + 2 ) + 2. ( 3 + 2 ) + 3. ( 4 + 2 ) + . . . + n . [ ( n + 1 ) + 2 ] S = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) + ( 1.2 + 2.2 + 3.2 + . . . . + n .2 ) Đặt A = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) 3 A = 1.2.3 + 2.3. ( 4 − 1 ) + . . . . + n . ( n + 1 ) . [ ( n + 2 ) − ( n − 1 ) 3 A = 1.2.3 + 2.3.4 − 1.2.3 + . . . . + n . ( n + 1 ) . ( n + 2 ) − ( n − 1 ) . n . ( n + 1 ) 3 A = n . ( n + 1 ) . ( n + 2 ) A = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. ( 1 + 2 + 3 + . . . + n ) S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. n . ( n + 1 ) : 2 S = n . ( n + 1 ) . ( n + 2 ) : 3 + n . ( n + 1 ) S = n . ( n + 1 ) . [ ( n + 2 ) : 3 + 1 )
D = 1^2 + 2^2 + 3^2 + ... + n^2
= 1.( 2 - 1 ) + 2.( 3-1 ) + 3.( 4-1 ) + .... + n.[ ( n+ 1) - 1 ]
= 1.2 - 1 + 2.3 - 2 + 3.4 - 3 + .... + n.( n+1 ) - n
= [ 1.2 + 2.3 + 3.4 + ..... + n.( n + 1 ) ] - ( 1 + 2 + 3 + .... + n )
= { [ n.( n+1 ).( n+2 )] /3 } - { [ n.( n+1)] /2 }
= { n(n+1)(2n+1) }/ 6
Vậy.........
PT
1
PT
1
CM
21 tháng 6 2018
+ Với n = 1 :
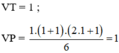
⇒ (3) đúng với n = 1
+ Giả sử đẳng thức (3) đúng với n = k nghĩa là :
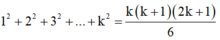
Cần chứng minh (3) đúng khi n = k + 1, tức là:
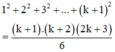
Thật vậy:
E
21 tháng 1 2022
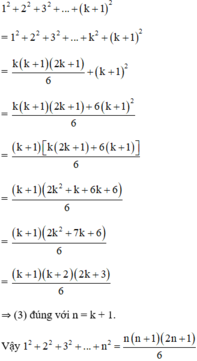
Với A1 = 12. Ta sẽ chứng minh An =1 + 3 + ... + (2n-1) = n2 (đáp án d)
Giả sử An đúng với n = k tức Ak = 1 + 3 + ... + (2k - 1) = k2. Ta sẽ chứng minh nó cũng đúng với Ak+1
Thật vậy: Ak+1 = 1 + 3 + ... + (2k-1) + (2k+1) = Ak + 2k + 1 = k2 + 2k + 1 = (k+1)2
Vậy...
18 tháng 1 2022
#include <bits/stdc++.h>
using namespace std;
long long n,i,s;
int main()
{
cin>>n;
s=0;
for (i=1; i<=n; i++) s=s+i*i;
cout<<s;
return 0;
}
KV
19 tháng 1 2022
Var s,i,n:longint;
Begin
Write('Nhap so luong so n = ');readln(n);
For i:=1 to n do
s:=s+i*i;
Write('Tong la ',s);
Readln;
End.
25 tháng 7 2017
- Xác định bài toán (0,5đ)
Input: Nhập N và dãy a 1 , a 2 , . . . , a n
Output: Đưa ra kết quả tổng S
- Thuật toán (1,75đ):
Bước 1: Nhập N và a 1 , a 2 , . . . , a n
Bước 2: S ← 0; i ← 1
Bước 3: Nếu i >Nthì đưa ra S rồi kết thúc
Bước 4: Nếu ai⟨0 thì S ←S+ a i 2
Bước 5: i ← i + 1 và quay lại Bước 3
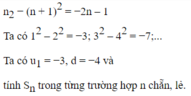
D=1212+2222+3232+....+ n2n2
D=1+ 2.(1+1) + 3.(2+1) +.....+ n(n-1 +1)
D=1 + 1.2 +2 + 2.3 + 3 +.......+ (n-1).n + n
D= (1 + 2 +3 +....+n) + (1.2 + 2.3 + 3.4 + ......+ (n-1)n )
D= n(n+1)2n(n+1)2 + n(n+1)(n−1)3n(n+1)(n−1)3
D= 3n(n+1)+2n(n+1)(n−1)63n(n+1)+2n(n+1)(n−1)6
D= n(n+1)(2n+1)6