Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(-3;6\right)\)
\(\overrightarrow{AC}=\left(-3,5;7\right)\)
Vì \(\overrightarrow{AB}=\dfrac{7}{6}\overrightarrow{AC}\)
nên A,B,C thẳng hàng

\(\overrightarrow{AB}=\left(-4;-12\right)\)
\(\overrightarrow{AC}=\left(-1;-6\right)\)
Vì -4/-1<>-12/-6
nên A,B,C ko thẳng hàng


Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: 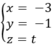

Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
\(\overrightarrow{AB}\left(2;1\right);\overrightarrow{BC}\left(-3;1\right);\overrightarrow{CA}\left(1;-2\right)\)
\(ptts:\)
\(d_{AB}:\left\{{}\begin{matrix}x=2+2t\\y=t\end{matrix}\right.\)
\(d_{BC}:\left\{{}\begin{matrix}x=4-3t\\y=1+t\end{matrix}\right.\)
\(d_{CA}:\left\{{}\begin{matrix}x=1+t\\y=2-2t\end{matrix}\right.\)
\(pttq:\)
\(d_{AB}:-1\left(x-2\right)+2y=0\Leftrightarrow2y-x+2=0\)
\(d_{BC}:x-4+3\left(y-1\right)=0\Leftrightarrow x+3y-7=0\)
\(d_{CA}:2\left(x-1\right)+y-2=0\Leftrightarrow2x+y-4=0\)
b/ \(\overrightarrow{MB}=\overrightarrow{CM}\Rightarrow M\left(\dfrac{x_B+x_C}{2};\dfrac{y_B+y_C}{2}\right)\Rightarrow M\left(\dfrac{5}{2};\dfrac{3}{2}\right)\)
\(\Rightarrow\overrightarrow{AM}\left(\dfrac{1}{2};\dfrac{3}{2}\right)\Rightarrow\overrightarrow{n_{AM}}=\left(-\dfrac{3}{2};\dfrac{1}{2}\right)\)
\(\Rightarrow d_{AM}:-\dfrac{3}{2}\left(x-2\right)+\dfrac{1}{2}y=0\Leftrightarrow\dfrac{1}{2}y-\dfrac{3}{2}x+3=0\)