Cho \(\Delta ABC\)vuông tại A. Biết 3AB = 4AC và BC = 20cm. Tính độ dài các cạnh AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có \(\dfrac{AB}{4}=\dfrac{AC}{3}\Rightarrow\dfrac{AB^2}{16}=\dfrac{AC^2}{9}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{AB^2}{16}=\dfrac{AC^2}{9}=\dfrac{BC^2}{25}=\dfrac{25^2}{25}=25\Rightarrow AB=20cm;AC=15cm\)

bai toan dang hieu va ty cua lop 4 do bạn;
ab/ac = 3/4
ab-ac =2
ab =6
ac=8

Ta có: \(\Delta\)ABC vuông tại A => \(AB^2+AC^2=BC^2=400\)
Ta có: \(\frac{AB}{3}=\frac{AC}{4}\Leftrightarrow\frac{AB^2}{9}=\frac{AC^2}{16}=\frac{AB^2+AC^2}{9+16}=\frac{400}{25}=16\)
\(\Rightarrow\hept{\begin{cases}AB^2=16.9=144\\AC^2=16^2\end{cases}}\)=> AB=12 và AC=16


a.
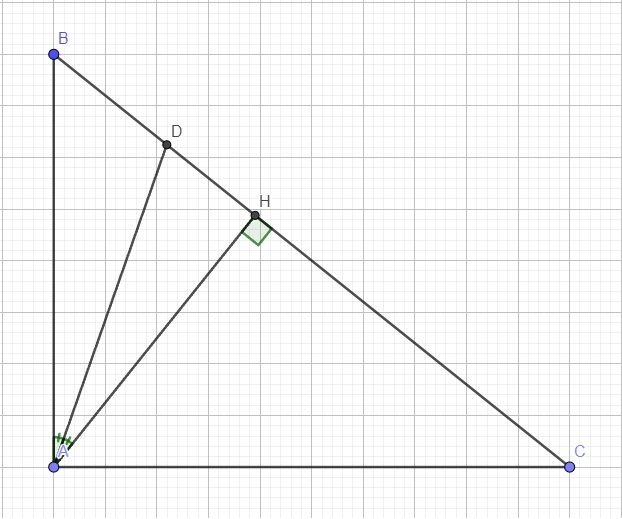
Xét hai tam giác HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BHA}=\widehat{BAC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Từ câu a ta có: \(\dfrac{HA}{AC}=\dfrac{BA}{BC}\Rightarrow HA=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
c.
Áp dụng định lý Pitago cho tam giác vuông HBA:
\(BH=\sqrt{AB^2-HA^2}=9\left(cm\right)\)
Do AD là phân giác, áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DH}{AH}\Rightarrow\dfrac{BD}{AB}=\dfrac{BH-BD}{AH}\)
\(\Rightarrow12BD=15\left(9-BD\right)\Rightarrow BD=5\left(cm\right)\)
\(\Rightarrow DH=BH-BD=4\left(cm\right)\)
đặt AC=3k;AB=4k(k>0)
ta có: (AC)^2+(AB)^2=BC^2
hay: 25k^2=400
nên: K^2=4^2 HAY K=4
nên: AC=16;AB=12
sorry mình bất cẩn tí rồi AB=16;AC=12