Cho tam giác ABC có AB < AC, hai đường cao BD và CE.
a, Chứng minh: T.giác ABD đồng dạng t.giác ACE.
Suy ra: AB.AE = AC.AD
b, Chứng minh: T.giác ADE đồng dạng t.giác ABC.
c, Tia DE và CB cắt nhau tại I. Chứng minh: t.giác IBE đồng dạng t.giác IDC.
d, Gọi O là trung điểm của BC. Chứng minh: ID.IE = OI2 - OC2.

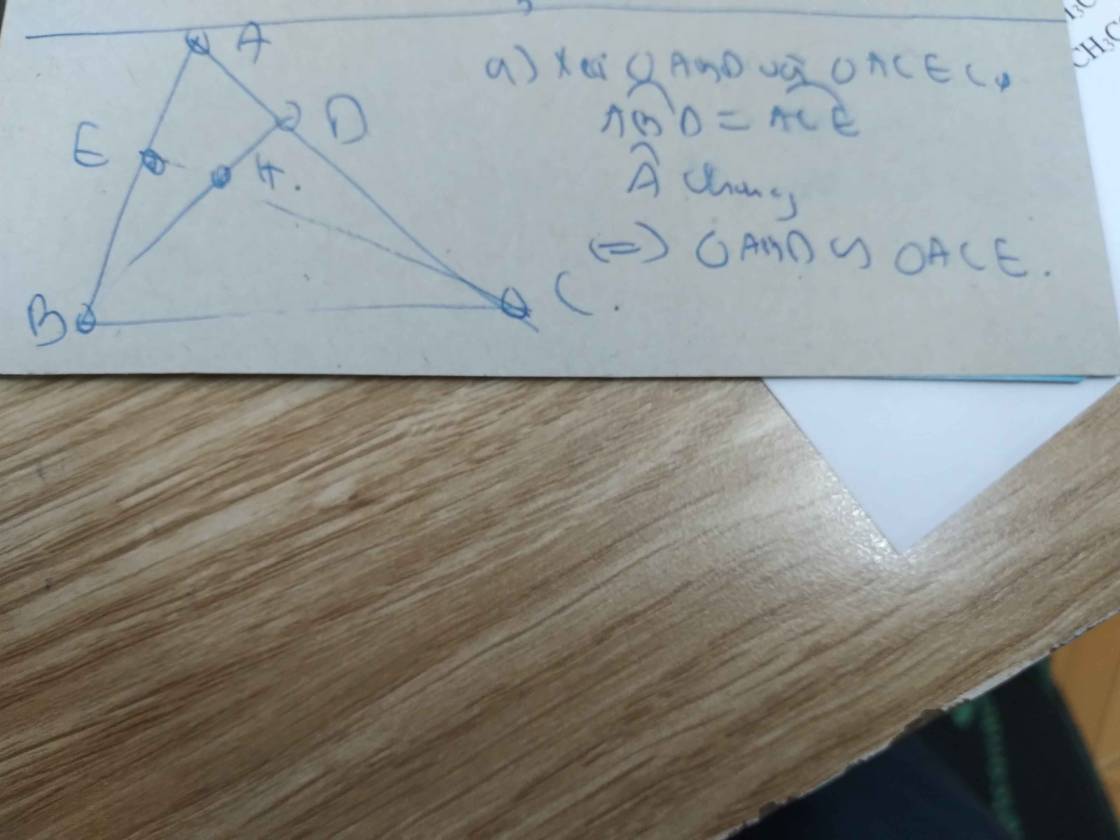

a : xét tg ABD và tg ACE có :
góc A chung
góc BAD = góc CEA (=90 độ)
ngoặc 2 dòng trên suy ra tg ABD đồng dạng vs tg ACE (g.g)