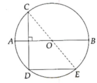
cho đường tròn tâm O đường kính AB .Vẽ góc ở tâm \(\widehat{AOC}\) =50 độ . Vẽ dây CD \(\perp\)AB và dây DE//AB
a)Tính số đo cung nhỏ BE
b)Tính số đo \(\stackrel\frown{CBE}\) từ đó suy ra 3 điểm C,O,E thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 8 2017
a, Tính được sđ B E ⏜ = 50 0
b, Chứng minh được sđ
C
B
E
⏜
=
180
0
=> C, O, E thẳng hàng (ĐPCM)
22 tháng 2 2021
a) Ta có: AB//DE(gt)
CD⊥AB(gt)
Do đó: DE⊥CD(Định lí 2 từ vuông góc tới song song)
⇔\(\widehat{CDE}=90^0\)
Xét ΔCDE có \(\widehat{CDE}=90^0\)(cmt)
nên ΔCDE vuông tại D(Định nghĩa tam giác vuông)
⇔D nằm trên đường tròn đường kính CE
⇔C,D,E nằm trên đường tròn đường kính CE
mà C,D,E cùng nằm trên (O)(gt)
nên CE là đường kính của (O)
hay C,O,E thẳng hàng(đpcm)
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
a. Câu hỏi chưa rõ ràng
b. Vì số đo cung nhỏ AB bằng một nửa số đo cung lớn AB mà tổng số
đo 2 cung bằng $360^0$ nên số đo cung nhỏ $AB$ là $120^0$
Từ $O$ kẻ $OH\perp AB$ như hình. Tam giác $OAB$ cân tại $O$ nên đường cao $OH$ đồng thời là đường phân giác, trung tuyến.
Do đó: $\widehat{AOH}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.120^0=60^0$
$\frac{AH}{AO}=\sin \widehat{AOH}=\sin 60^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AH=\frac{\sqrt{3}}{2}AO=\frac{\sqrt{3}}{2}R$
$\Rightarrow AB=2AH=\sqrt{3}R$
Tự vẽ hình
a) Do \(CD\) vuông góc \(AB\) nên \(AB\) là trung trực của \(CD\) (liên hệ giữa đường kính và dây cung)
\(\Rightarrow AC=AD\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Mà \(sđ\stackrel\frown{AC}=\stackrel\frown{AOC}=50^0\Rightarrow sđ\stackrel\frown{AD}=50^0\).
Do \(DE\) song song \(AB\)
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{AD}=50^0\Rightarrow\widehat{BOE}=sđ\stackrel\frown{BE}=50^0\).
b) Do \(B\in\stackrel\frown{CE}\Rightarrow sđ\stackrel\frown{CBE}=sđ\stackrel\frown{CB}+sđ\stackrel\frown{BE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=\widehat{COB}+\widehat{BOE}=180^0-\widehat{AOC}+\widehat{BOE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=180^0-50^0+50^0=180^0\)
\(\Rightarrow\) CE là đường kính
\(\Rightarrow\) C, O, E thẳng hàng.