Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi giao điểm của AC và EF là O
có EO//CD(EF//CD;O\(\in\)EF)
=>\(\frac{AE}{AD}=\frac{EO}{CD}\)(hệ quả ta-lét)
=>\(\frac{1}{3}=\frac{EO}{4}\left(CD=4cm;\frac{AE}{AD}=\frac{1}{3}\right)\)
=> EO=\(\frac{4}{3}\)cm
có BF=\(\frac{1}{3}\)BC(gt)=>CF=(1-\(\frac{1}{3}\))BC=\(\frac{2}{3}\)BC
Có FO//AB(EF//CD;O\(\in\)EF)
=>\(\frac{CF}{CB}=\frac{FO}{AB}\)(hệ quả talet)
=>\(\frac{2}{3}=\frac{FO}{1}\left(\frac{CF}{CB}=\frac{2}{3};AB=1cm\right)\)
=>FO=\(\frac{2}{3}\)cm
Có EO+FO=EF(O\(\in\)EF)
=>EF=\(\frac{4}{3}\)+\(\frac{2}{3}\)=\(\frac{6}{3}\)=2cm
vậy độ dài EF=2cm

Gọi AB là a, CD là b
Ta có b - a = 3.5 (1)
b = 5/4 a (2)
Thay 2 vào 1, giải ra được a = 14 , b = 17.5
Sau đó tính diện tích hình thang abcd theo công thức bình thường
b, Kẻ BN vuong góc với cd cắt eg tại m
Dễ dàng suy ra được EN = AB = 14
Dễ dàng suy ra được NC = CD - AB = 3.5
Dễ dàng suy ra được MN = 3 , Bn = 7
=> NG = 7/10 . 3.5 = 2.45
=> EG = 16.45
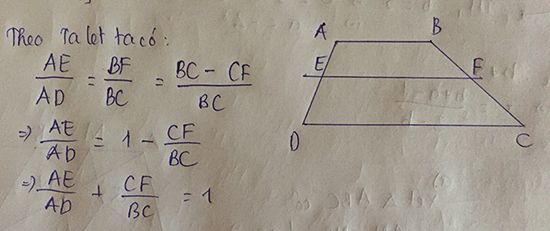 Đây nha !!
Đây nha !!