Cho một tam giác vuông với cạnh huyền có chiều dài c, độ dài hai cạnh góc vuông lần lượt là a và b \(\left(c>a,b>0\right)\). Từ a và b ta lập 2 hình chữ nhật đều có độ dài hai kích thước là a và b. Chứng minh rằng diện tích của hình vuông cạnh c luôn lớn hơn hoặc bằng tổng diện tích của 2 hình chữ nhật vừa lập được. Tam giác vuông ban đầu cần có thêm điều kiện gì để trường hợp bằng xảy ra?

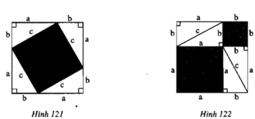



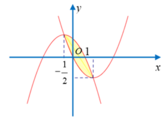
Diện tích hình vuông cạnh c là \(S=c^2\)
Tổng diện tích hai hình chữ nhật là \(S_1=2ab\)
Xét tg vuông có \(c^2=a^2+b^2\)
Áp dụng cosi có
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\frac{a^2+b^2+2ab}{4}\ge ab\Rightarrow a^2+b^2\ge2ab\) Dấu = xảy ra khi \(a=b\)
\(\Rightarrow S\ge S_1\left(dpcm\right)\)
\(S=S_1\) Khi a=b => tg ban đầu phải là tg vuông cân