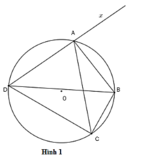
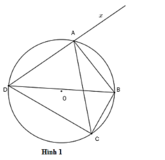
Cho tứ giác ABCD nội tiếp đường tròn (O;R). Gọi a, b, c, d lần lượt là độ dài các cạnh AB, BC, CD, DA ; G là trọng tâm của tứ giác, T là điểm đối xứng của G qua O. Chứng minh rằng TA + TB +TC +TD \(\ge4R\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
9 tháng 5 2022
Ta có: `hat(ABD) = hat(ACD)`.
Lấy `M in AC` sao cho `hat(ADB) = hat(MDC)`.
`=> triangle ABD ~ triangle MCD`.
`=> (AB)/(MC) = (BD)/(CD) => AB . CD = BD . MC`.
Xét `2 triangle ADM, BDC`, ta có:
`hat(ADM) = hat(BDC)`.
`(DA)/(DM) = (BD)/(DC) ( triangle ABD ~ triangle MCD )`.
`=> triangle ADM ~ triangle BCD => (AD)/(AM) = (BD)/(CB) => AD . BC = BD . AM`
`=> AD . BC + AD . BC = BD . AM + BD . MC`
`=> AD . BC + AD . BC = BD(AM+MC)`
`=> AD.BC+AD.BC = BD . AC => dpcm`.
CM
16 tháng 1 2018
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
CM
23 tháng 1 2017
Chọn đáp án D
(góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó )
Phương án A, B, C đúng
22 tháng 3 2021
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
FF
1
26 tháng 2 2018
Đây là đẳng thức ptôlêmê.
C/m: Lấy 1 điểm M thuộc AC sao cho gocABD=gocMBC. Do tứ giác ABCD nội tiếp nên ^ADC=^ACB. Từ 2 điều trên suy ra tam giác ABD ~ MBC(g.g). Suy ra AD/MC=BD/BC => AD.BC=BD.MC (1)
Từ cặp tam giác đồng dạng trên ta cũng có AB/BM = BD/BC => AB/BD = BM/BC mà ^ABM = ^DBC nên tam giác ABM ~ tam giác DBC.
=> AB.CD=AM.BD (2)
Cộng (1), (2) vế theo vế suy ra AC.BD = AB . CD + AD . BC
Vậy AC.BD = AB.CD + AD . BC ( đpcm )
N
0
