7.cho tam giác ABC (AB<AC) , đường cao AK .gọi D,E,F theo thứ tự là trung điểm của AB ,AC , BCa) tứ giác BDEF là hình j ? vì saob)cm tứ giác DEFK là hình thang cân c) Gọi H là trực tâm của tam giác ABC ; M,N,P theo thứ tự là trung điểm của HA , HB,HC .cm các đoạn thẳng MF ,NE ,PD bằng nhau và cắt nhau tại trung điểm của mỗi...
Đọc tiếp
7.cho tam giác ABC (AB<AC) , đường cao AK .gọi D,E,F theo thứ tự là trung điểm của AB ,AC , BC
a) tứ giác BDEF là hình j ? vì sao
b)cm tứ giác DEFK là hình thang cân
c) Gọi H là trực tâm của tam giác ABC ; M,N,P theo thứ tự là trung điểm của HA , HB,HC .cm các đoạn thẳng MF ,NE ,PD bằng nhau và cắt nhau tại trung điểm của mỗi đoạn
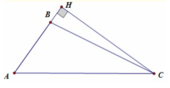
a/ Xét t/g ABC có D,E lần lượt là trung điểm AB ; AC
=> DE là đường trung bình t/g ABC
=> DE // BC ; DE = BC/2
=> DE // BF ; DE = BF(do F là trung điểm BC)
=> Tứ giác BDEF là hình bình hành
b/ Có BDEF là hbh
=> EF = BD
Xét t/g ABK vuông tại K có KD là đường trung tuyến
=> KD = 1/2 AB = BD=> EF = KD
Mà DE // BC
=> DE // KF
=> Tứ giác DEFK là htc
c/ Xét t/g AHC có ME là đường trung binh
=> ME = 1/2 HC ; ME // HC (1)
Xét t/g BHC có NF là đường trung bình
=> NF = 1/2 HC ; NF // HC (2)
(1) ; (2)
=> ME = NF ; ME // NF (3)
Xét t/g ABH có MN là đường trung bình
=> MN // AB ; MN = 1/2 ABMà
HC ⊥ AB
NF // HC=> MN ⊥ NF (4)(3) ; (4)
=> MNFE là hcn
=> NE = MF ; NE, MF cắt nhau tại trung điểm mỗi đoạn
CMTT ta có đpcm