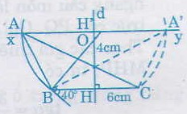
(Bài 49 SGK toán 9 tr.87) Dựng tam giác ABC, biết BC = 6 cm, \(\widehat{A}=40^\circ\) và đường cao AH = 4cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là ,
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là \(\widehat{A}\) , \(\widehat{A'}\). Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán


Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40 º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 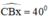
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40 º dựng trên đoạn BC
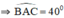
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

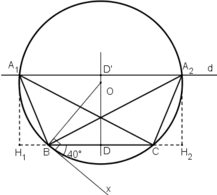
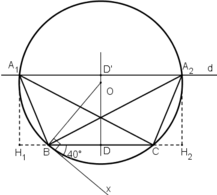
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho 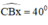
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
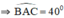
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.

AMAM là đường trung tuyến ứng với cạnh huyền nên AM=BC2=BMAM=BC2=BM
⇒△MAB⇒△MAB cân tại MM
⇒BAMˆ=MBAˆ⇒BAM^=MBA^
Ta có:
BADˆ=DAMˆ−BAMˆ=900−MBAˆ=900−HBAˆBAD^=DAM^−BAM^=900−MBA^=900−HBA^
HABˆ=900−HBAˆHAB^=900−HBA^
⇒BADˆ=HABˆ⇒BAD^=HAB^ nên ABAB là tia phân giác DAHˆDAH^ (đpcm)
b)
Xét tam giác CADCAD và ABDABD có:
DˆD^ chung
ACDˆ=900−ABHˆ=BADˆACD^=900−ABH^=BAD^
⇒△CAD∼△ABD⇒△CAD∼△ABD (g.g)
⇒CAAB=ADBD=CDAD⇒CAAB=ADBD=CDAD
⇒CA2AB2=CDBD(∗)⇒CA2AB2=CDBD(∗)
Dễ thấy △BAH∼△BCA△BAH∼△BCA (g.g) và △CAH∼△CBA△CAH∼△CBA (g.g)
⇒BABC=BHBA⇒BABC=BHBA và CACB=CHCACACB=CHCA
⇒AB2=BC.BH⇒AB2=BC.BH và AC2=CH.BCAC2=CH.BC
⇒AC2AB2=CHBH(∗∗)⇒AC2AB2=CHBH(∗∗)
Từ (∗);(∗∗)⇒CDBD=CHBH(∗);(∗∗)⇒CDBD=CHBH
⇒CD.BH=CH.BD⇒CD.BH=CH.BD (đpcm)

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

Hướng dẫn làm bài:
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1cm
Tâm O của đường tròn nội tiếp ∆ABC là giao điểm của đường thẳng (d) với cung chứa góc 90° + 60° : 2 = 120° dựng trên đoạn BC cố định
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A. Tam giác ABC là tam giác phải dựng
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
Tâm O của đường tròn nội tiếp tam giác ABC là giao điểm của đường thẳng (d) với cung chứa góc 90o + 60o : 2 = 120o dựng trên đoạn BC cố định.
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A.
Tam giác ABC là tam giác cần dựng.
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là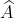 ,
, 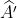 . Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.