Trên đường tròn (O) lấy ba điểm A, B và C. Gọi M, N và P theo thứ tự là điểm chính giữa các cung AB, BC và AC. BP cắt AN tại I, NM cắt AB tại E. Gọi D là giao điểm của AN và BC. Chứng minh rằng:
a) Tam giác BNI cân;
b) AE.BN = EB.AN;
c) EI // BC;
d) $\dfrac{AN}{BN}=\dfrac{AB}{BD}$.

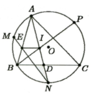

a) ta có :
P là điểm chính giữa cung AC
=> cung AP = cung PC
N là điểm chính giữa cung BC
=> cung NB = NC
Mà : góc IBN = 1/2 cung PN = 1/2 (cung PC + cung CN )
góc BIN = 1/2 ( cung BN + AP )
mà cung PC = cung AP
cung BN = cung CN
=> IBN = BIN
=> tam giác IBN là tam giác cân
b) ta có : N là điểm chính giữa của cung BC
=>MN là tia phân giác của góc BAC
=> EB/AE=BN/AN
=> đpcm
c) ta có : BNI cân
NM là tia phân giác
=> NM cũng là tia trung trực
=> EBN = EIN
MÀ IBN = BIN ( tam giác cân )
=> EBI=EIB (1)
=> tam giác EBI cân
mà P là điểm chính giữa cung AC
=> BP là đường phân giác của góc EBN
=> EBP = IBN hay EBI=IBN (2)
từ (1) và (2) => IBN=EIB
mà 2 góc ở vị trí slt => EI//BC
d) Xét tam giác BAN và tam giác BDN
có N chung
góc BAN = BDN ( cùng chắn cung BN )
=> tam giác BAN đồng dạng tam giác BDN
=> đpcm
a, CM BIN=IBN = 1/2 sđ PN => tam giác BIN cân tại N
b, CM đc MN vuông góc với BP mà tam giác BIN cân tại N => MN là đường trung trực của BI , E thuộc MN => BE=BI và EN là tia pg của BEI
CM tam giác AEN ~ tam giác IEN ( g-g) =>AE.IN = EI.AN => AE.BN = EB.AN
c, CM đc EBP = PBC mà EBI =EIB nên EIB = IBD mà 2 góc này ở vị trí slt=> EI //BC
d, CM tam giác ABN~ tam giác BDN ( g-g) => AN/BN = AB /BD \dfrac{AN}{BN}=\dfrac{AB}{BD}