Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chứng minh thuận:
Đường tròn (O) cho trước, điểm A cố định nên OA có độ dài không đổi.
ΔOBC cân tại O (vì OB = OC bán kính)
IB = IC (gt) nên OI là đường trung tuyến vừa là đường cao
OI ⊥ BC
Góc OIA = 90 °
Đường thẳng d thay đổi nên B, C thay đổi thì I thay đổi tạo với 2 đầu đoạn OA cố định góc góc OIA = 90 ° . Vậy I chuyển động trên đường tròn đường kính OA.
Chứng minh đảo: Lấy điểm I’ bất kỳ trên đường tròn đường kính AO. Đường thẳng AI’ cắt đường tròn (O) tại 2 điểm B’ và C’.
Ta chứng minh: I’B = I’C’.
Trong đường tròn đường kính AO ta có góc OI'A = 90 ° (góc nội tiếp chắn nửa đường tròn)
OI'⊥ B'C'
I'B' = I'C' (đường kính vuông góc với dây cung)
Vậy quỹ tích các điểm I là trung điểm của dây BC của đường tròn tâm O khi BC quay xung quanh điểm A cố định là đường tròn đường kính AO.
Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
Cho đường tròn tâm bán kính và một điểm nằm ngoài đường tròn. Kẻ một đường thẳng đi qua và không đi qua , cắt đường tròn tại hai điểm phân biệt , ( nằm giữa và ). Từ vẽ hai tiếp tuyến và với (, là hai tiếp điểm). Đường thẳng cắt tại . Gọi là trung điểm của . Đường thẳng cắt đường thẳng tại . Chứng minh là tứ giác nội tiếp.
theo gt, ta co:
là trung điểm của
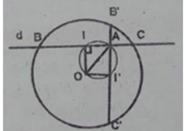
a) = AI2
b) điểm D như hình vẽAD=AI2/AB= constant.
Ta có PQI = PIA ( cùng chắn PI) nên ΔAPI ~ΔAIQ(g.g）
=> AP/AI = AI/AQ =>Ap.AQ= AI^2 ( không đổi )
Giả sử đt ngoại tiếp tấm giác BPQ cắt AB tại D (D khác B)
Khi đó tam giác ADP ~ tam giác AQB =>AD/AQ = AP/AB
hay AD.AB = AP.AQ=AI^2 ( không đổi)
Do đó điểm D là điểm cố định (đpcm)