Cho hình bình hành ABCD có AB=a, BC=b, DB=m và AC=n. Chứng minh rằng \(^2m+n^2=2\left(a^2+b^2\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)

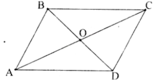
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
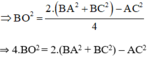
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).

Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm

Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!

a) Ta có : tứ giác ABCD là hình bình hành (gt)
\(\Rightarrow\)2 đường chéo cắt nhau tại trung điểm của mỗi đường
\(\Rightarrow\)O là trung điểm của AC (1)
và O là trung điểm của BD
\(\Rightarrow OB=OD\)
mà \(DE=BF\left(gt\right)\)
\(\Rightarrow OB-BF=OD-DE\)
\(\Rightarrow OF=OE\)
\(\Rightarrow\)O là trung điểm của EF (2)
Từ (1) và (2) \(\Rightarrow\)tứ giác AECF là hinh bình hành
b) Ta có : tứ giác AECF là hinh bình hành (cma)
\(\Rightarrow AE//CF\)
\(\Rightarrow AM//CN\left(3\right)\)
Ta có : tứ giác ABCD là hinh bình hành (gt)
\(\Rightarrow AB//CD\)
\(\Rightarrow AN//CM\left(4\right)\)
TỪ (3) và (4) \(\Rightarrow\)tứ giác ANCM là hình bình hành
\(\Rightarrow AM=CN\)
c) Ta có : tứ giác ANMC là hinh bình hành (cmb)
\(\Rightarrow\)2 đường chéo cắt nhau tại trung điểm của mỗi đường
\(\Rightarrow\)O là trung điểm của NM
và O là trung điểm của AC
mà O là trung điểm của BD
\(\Rightarrow\)AC , NM , DB cùng đi qua 1 điểm

1.
AB=CD (cặp cạnh đối hbh)
AM=AB/2 và CN=CD/2
=> AM=CN (1)
AM thuộc AB; CN thuộc CD mà AB//CD => AM//CN (2)
Từ (1) và (2) => AMCN là hbh(Tứ giác có một cặp cạnh đối // và = nhau thì tứ giác đó là hbh)
2.
a. M là trung điểm AB; N là trung điểm AC => MN là đường trung bình của tgABC
=> MN//BC => MN//BP và MN=BP=BC/2
=> BMNP là hbh (lý do như bài 1)
b. Ta có BMNP là hbh và ^B=90 => BMNP là HCN
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^2}=4cm.\)
Từ kq câu a => MN=BC/2=4/2=2 cm
C/m tương tự câu a có NP là đường trung bình của tg ABC => NP=AB/2=3/2=1,5 cm
Chu vi BMNP là
(2+1,5)x2=7 cm
ta có \(\hept{\begin{cases}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\Rightarrow AC^2=AB^2+BC^2+2\overrightarrow{AB}.\overrightarrow{BC}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}\Rightarrow BD^2=BA^2+AD^2+2\overrightarrow{BA}.\overrightarrow{AD}\end{cases}}\)
mà \(\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{BA}.\overrightarrow{AD}=\overrightarrow{AB}.\overrightarrow{BC}+\overrightarrow{AB}.\overrightarrow{AD}=0\)
Do đó \(AC^2+BD^2=2AB^2+2BC^2\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)