Một xí nghiệp nhà máy nhận làm một lượng công việc. Tuy nhiên khi bắt đầu làm công việc thì khối lượng làm công việc lại phát sinh và tăng lên 21%, trong đó năng suất năng lượng chỉ tăng lên 10%. Vậy để hoàn thành công việc đó đúng thời hạn thì phải tăng số công nhân lên bao nhiêu phần trăm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Coi khối lượng công việc cũ là 100% thì khối lượng công việc mới bằng:
100% + 40% = 140% = 1,4 (khối lượng công việc cũ)
Coi năng suất lao động cũ là 100% thì năng suất lao động mới bằng:
100% + 25% = 236% = 1,25 (năng suất công việc cũ)
Ta có :
Số công nhân = Khối lượng công việc : năng suất lao động nên số công nhân mới bằng:
1,4 : 1,25 = 1,12 = 112% (số công nhân cũ)
Coi số công nhân cũ là 100% thì số phần trăm công nhân phải tăng thêm là:
112% - 100% = 12% (số công nhân cũ)
Đáp số: 12%

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)
Điều kiện : x, y > 12, x,y ∈ N.
Một ngày đội I làm được : 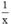 (công việc).
(công việc).
Một ngày đội II làm được :  (công việc).
(công việc).
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: 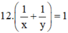
+ Hai đội cùng làm trong 8 ngày được: 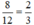 công việc.
công việc.
⇒ còn lại đội II phải hoàn thành một mình 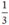 công việc.
công việc.
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 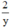 công việc.
công việc.
Đội II hoàn thành 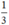 công việc còn lại trong 3,5 ngày nên ta có phương trình:
công việc còn lại trong 3,5 ngày nên ta có phương trình: 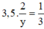
Ta có hệ phương trình:
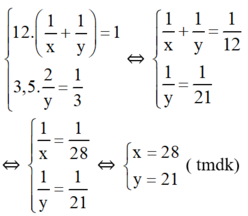
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)
Điều kiện : x, y > 12, x,y ∈ N.
Một ngày đội I làm được : 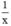 (công việc).
(công việc).
Một ngày đội II làm được :  (công việc).
(công việc).
+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: 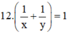
+ Hai đội cùng làm trong 8 ngày được: 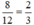 công việc.
công việc.
⇒ còn lại đội II phải hoàn thành một mình 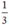 công việc.
công việc.
Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 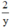 công việc.
công việc.
Đội II hoàn thành 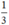 công việc còn lại trong 3,5 ngày nên ta có phương trình:
công việc còn lại trong 3,5 ngày nên ta có phương trình: 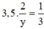
Ta có hệ phương trình:
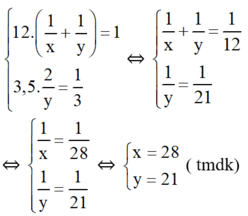
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

-Gọi số tấm thảm làm trong 1 ngày theo dự định là x (tấm, x ϵ N*)
-Tổng số tấm thảm làm theo dự định là 20x (tấm)
-Thực tế tăng 20% nên trong 1 ngày làm được :
x+20%x = 1,2x(tấm)
-Thực tế làm được tổng : 1,2x . 18 = 21,6x (tấm)
⇒PT: 21,6x - 20x =24
⇔1,6x =24
⇔x=15 (TM)
⇒Số thảm làm trong 18 ngày là: 324 (tấm)

Gọi số ngày đội làm việc để xong công trình là x ( ngày )
Theo đề bài ta có: số công nhân và số ngày là 2 đại lượng tỉ lệ nghịch
\(\Rightarrow\dfrac{x}{35}=\dfrac{20}{35+15}=\dfrac{20}{50}\)
\(\Rightarrow x=\dfrac{35\times20}{50}=14\) ( ngày )
Vậy đội đó làm xong trong 14 ngày

Coi khối lượng công việc cũ là 100% thì khối lượng công việc mới bằng:
100% + 40% = 140% = 1,4 (khối lượng công việc cũ)
Coi năng suất lao động cũ là 100% thì năng suất lao động mới bằng:
100% + 25% = 236% = 1,25 (năng suất công việc cũ)
Ta có : Số công nhân = Khối lượng công việc : năng suất lao động nên số công nhân mới bằng:
1,4 : 1,25 = 1,12 = 112% (số công nhân cũ)
Coi số công nhân cũ là 100% thì số phần trăm công nhân phải tăng thêm là:
112% - 100% = 12% (số công nhân cũ)
Đáp số: 12%
Coi khối lượng công việc ban đầu là 100%; năng suất lao động ban đầu là 100% và số công nhân ban đầu là 100%.
Sau khi khối lượng công việc tăng 40% thì là:
100%+40%=140%
Sau khi năng suất lao động tăng 25% thì là:
100%+25%=125%
Số công nhân là:
140%:125%=112%
=>số công nhân phải tăng:
112%-100%=12%

Làm trong 21 ngày cần \(15\times35:21=25\left(máy\right)\)
Vậy cần thêm \(25-15=10\left(máy\right)\)