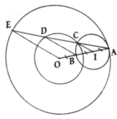
cho đường tròn (O) đường kính A.Trên đường tròn lấy điểm C sao cho AC<BC (C khác A).các tiếp tuyến tại B và C của đương tròn tâm O cắt nhau ở điểm D.AD cắt đường tròn tâm O tại E (E khác A).DO cắt BC tại F
a) Chứng minh BC vuông góc OD
b) chứng minh DF.DO=DE.DA

a) Xét (O) có
DB là tiếp tuyến có B là tiếp điểm(gt)
DC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: DB=DC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: DB=DC(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD\(\perp\)BC(đpcm)
b) Xét (O) có
ΔEAB nội tiếp đường tròn(E,A,B cùng thuộc đường tròn (O))
AB là đường kính(gt)
Do đó: ΔEAB vuông tại E(Định lí)
\(\Leftrightarrow\)BE\(\perp\)AE tại E
hay BE\(\perp\)DA
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDBA vuông tại B có BE là đường cao ứng với cạnh huyền DA, ta được:
\(DE\cdot DA=DB^2\)(1)
Ta có: DO\(\perp\)BC(cmt)
mà DO cắt BC tại F(gt)
nên BF\(\perp\)DO tại F
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDBO vuông tại B có BF là đường cao ứng với cạnh huyền DO, ta được:
\(DF\cdot DO=DB^2\)(2)
Từ (1) và (2) suy ra \(DF\cdot DO=DE\cdot DA\)(đpcm)