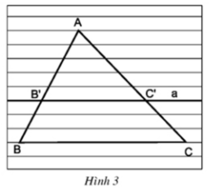
Chứng minh rằng: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\dfrac{B'B}{AB}=\dfrac{C'C}{AC}\)
\(\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}\)

a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)
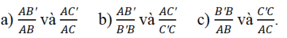
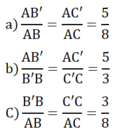
https://diendan.hocmai.vn/threads/chung-minh-dinh-li-talet.287639/