
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Xét \(\left(O\right):\)
+) Ta có: Dây AB = Dây AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}.\)
+) \(\widehat{ABM}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
Mà \(\stackrel\frown{AB}=\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\widehat{ABM}=\widehat{ABC}.\)
\(\Rightarrow\) BA là phân giác \(\widehat{CBM}.\)
b) Xét \(\left(O\right):\)
\(\widehat{MBA}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{MDB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc nội tiếp).
\(\Rightarrow\widehat{MBA}=\widehat{MDB}.\)
Xét \(\Delta MAB\) và \(\Delta MBD:\)
\(\widehat{MBA}=\widehat{MDB}.\)
\(\widehat{BMD}chung.\)
\(\Rightarrow\Delta MAB\sim\Delta MBD\left(g-g\right).\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{MB}{MD}\) (Cặp cạnh tương ứng tỉ lệ).
\(\Rightarrow MA.MD=MB^2.\)

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔABE đều

a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)

a: \(25x^2-16=0\)
=>(5x-4)(5x+4)=0
=>x=4/5 hoặc x=-4/5
b: \(-3x^2+18x=0\)
\(\Leftrightarrow3x^2-18x=0\)
=>3x(x-6)=0
=>x=0 hoặc x=6
\(25x^2-16=0\Leftrightarrow\left(5x\right)^2=16\)
\(\Leftrightarrow5x=\sqrt{4^2}=\left|4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=4\Leftrightarrow x=\dfrac{4}{5}\\5x=-4\Leftrightarrow x=\dfrac{-4}{5}\end{matrix}\right.\)
Vậy \(x=\pm\dfrac{4}{5}\)



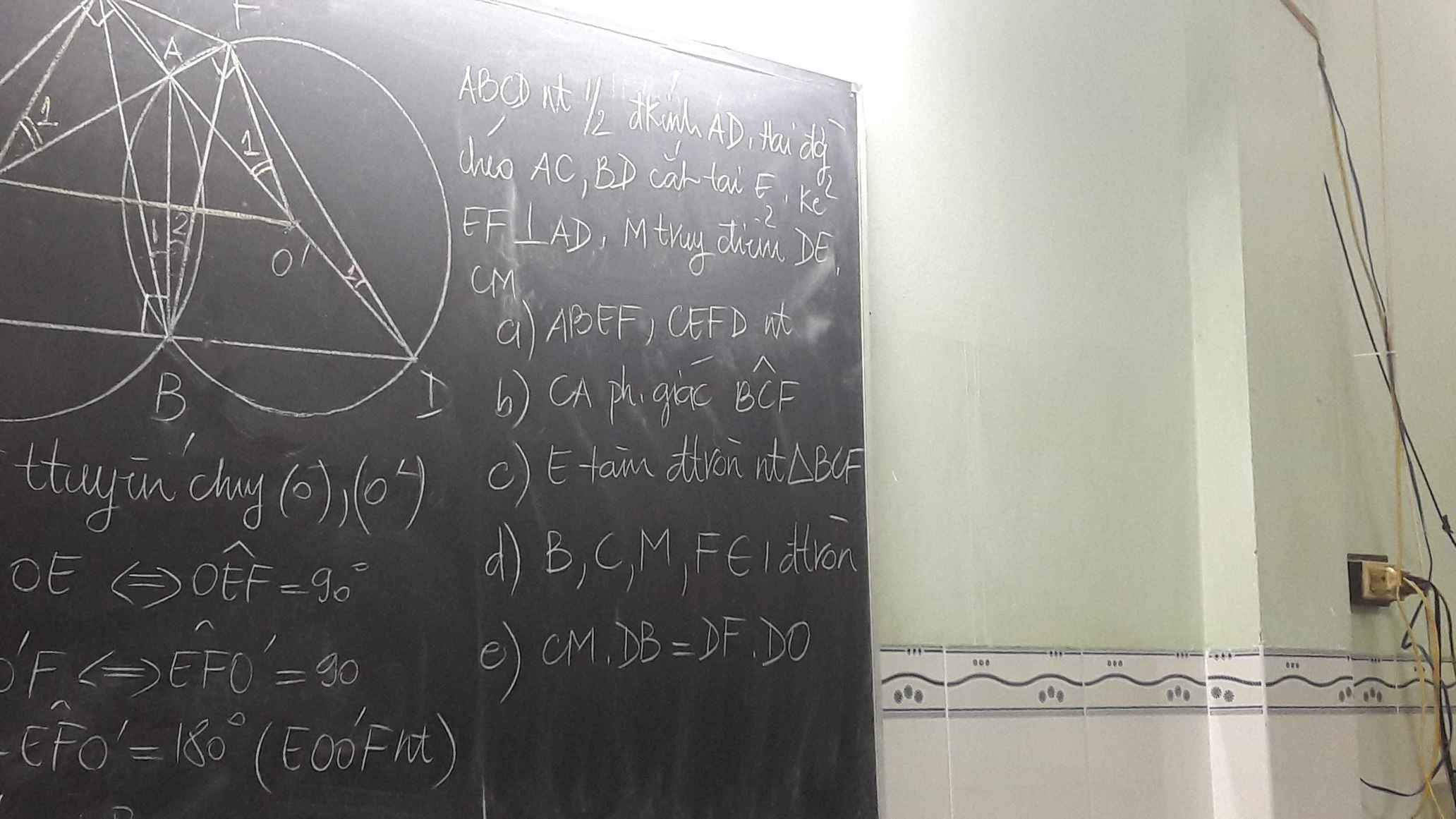

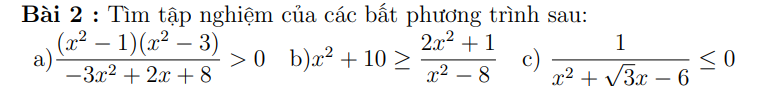
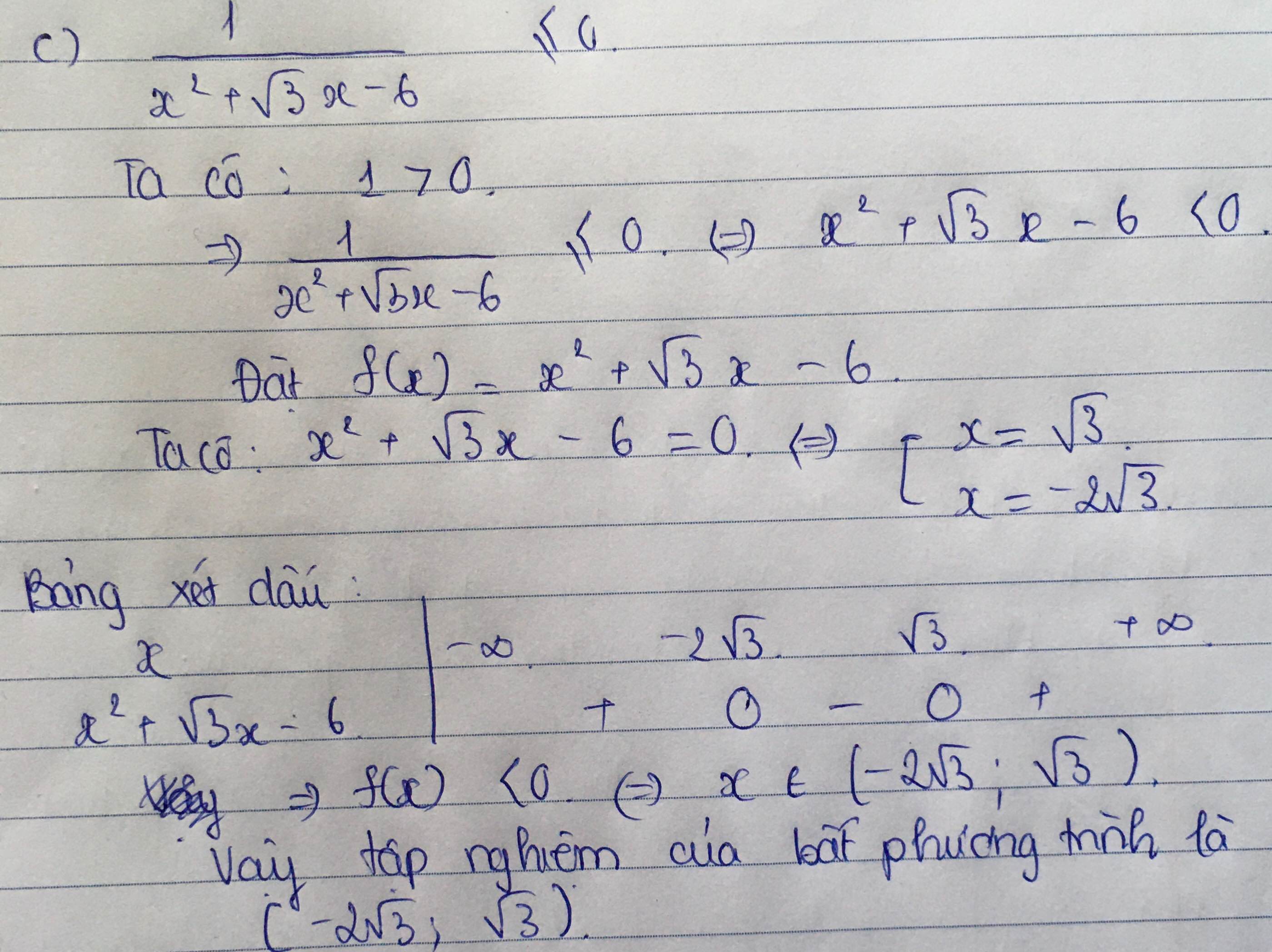


 giúp mình câu a, b, c trong chỗ bt vs ạ
giúp mình câu a, b, c trong chỗ bt vs ạ
