Cho tam giác ABC vuông tại A. E là trung điểm của BC. Gọi H là điểm đối xứng với E qua AC. Kẻ EM vuông góc AB tại M, gọi N là giao điểm của HE và AC. a) Vẽ hình, viết GT, KL của bài toán. b) Tứ giác ANEM là hình gì? c) Chứng minh tứ giác AECH là hình thoi? d) Tam giác ABC có điều kiện gì thì tứ giác ANEM là hình vuông?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ANEM có
\(\widehat{ANE}=\widehat{AME}=\widehat{MAN}=90^0\)
Do đó: ANEM là hình chữ nhật

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

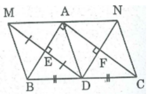
Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = 1/2 AB; AF = 1/2 AC
Nên AE = AF ⇒ AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

b: Ta có: A và H đối xứng nhau qua DF
nên DF là đường trung trực của AH
=>B là trung điểm của AH và DF⊥AH tại B
Xét tứ giác DBAC có
\(\widehat{ABD}=\widehat{ACD}=\widehat{BDC}=90^0\)
Do đó: DBAC là hình chữ nhật
c: Xét ΔDEF có
A là trung điểm của EF
AB//DE
Do đó: B là trung điểm của DF
Xét tứ giac DAFH có
B là trung điểm của DF
B là trung điểm của AH
Do đó: DAFH là hình bình hành
mà AD=AF
nên DAFH là hình thoi