3 bạn A,B,C mỗi bạn viết ngẫu nhiên lên bảng 1 số tự nhiên thuộc đoạn [1;16]. Xác suất để 3 số được viết ra có tổng chia hết cho 3 bằng?
Cho em hỏi cách làm dạng này với ạ :<
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số các số tự nhiên có 3 chữ số đôi một khác nhau thuộc tập X là: 5.4.3 = 60.
Trong đó số các số không có mặt chữ số 5 là 4.3.2 = 24 và số các số có mặt chữ số 5 là 60 - 24 = 36.
Gọi A là biến cố hai số được viết lên bảng đều có mặt chữ số 5; B là biến cố hai số được viết lên bảng đều không có mặt chữ số 5.
Rõ ràng A và B xung khắc. Do đó áp dụng quy tắc cộng xác suất ta có:
P A ∪ B = P A + P B = C 36 1 . C 36 1 C 60 1 . C 60 1 + C 24 1 . C 24 1 C 60 1 . C 60 1 = 13 25
Vậy xác suất cần tìm là
P = 1 - P A ∪ B = 1 - 13 25 = 12 25
Đáp án A

Tập S có tất cả 2 6 = 64 tập con. Mỗi bạn có 64 cách viết ngẫu nhiên. Nên số phần tử không gian mẫu bằng 64 3
Ta tìm số cách viết thoả mãn:
Gọi x, y, z là số phần tử có trong các tập con của A, B, C viết lên bảng.
Vì các tập con của ba bạn này viết khác rỗng nên x , y , z ≥ 1
Vì các tập con của ba bạn này đôi một không giao nhau và trên bảng có đúng 4 phần tử của S nên x+y+z=4
Vậy ta có hệ 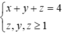
⇔ ( x ; y ; z ) = 1 ; 1 ; 2 ; 1 ; 2 ; 1 ; 2 ; 1 ; 1
Vậy có tất cả ![]() cách viết thoả mãn.
cách viết thoả mãn.
Xác suất cần tính bằng ![]()
Chọn đáp án B.

Ủa đề bài ko yêu cầu 3 chữ số khác nhau à? Thế thì dài lắm, rất phức tạp :(
Cách suy nghĩ về cơ bản như sau: gọi số A viết là \(\overline{abc}\), như vậy với mỗi số A viết B có 6 cách viết tương ứng (hoán vị 3 chữ số của A). Nhưng có 2 vấn đề rắc rối: 1/ trong các số a;b;c có mặt số 0, do đó khi hoán vị có khả năng 0 sẽ bị đẩy ra đứng đầu (không phù hợp). 2/ Trong có các a;b;c có ít nhất 2 chữ số giống nhau =>khi hoán vị sẽ bị lặp lại kết quả => thừa nghiệm. Do đó cần chia ra rất nhiều trường hợp và trong mỗi trường hợp lại chia nhỏ các trường hợp bên trong:
TH1: \(\overline{abc}\) chứa 2 số 0 \(\Rightarrow b=c=0\Rightarrow a\) có 3 cách chọn \(\Rightarrow\) có 3 số. Với mỗi số A viết, B có đúng 1 cách viết thỏa mãn (giống hệt A)
TH2: \(\overrightarrow{abc}\) chứa 1 số 0 tại vị trí b hoặc c. Giả sử \(c=0;b\ne0\)
\(\Rightarrow\)có \(3.3+3.3+3.3=27\) số. Hoán vị b và c có 2 cách \(\Rightarrow\) có \(27.2=54\) số, trong đó có 3 trường hợp một cặp số giống nhau (33;66;99) và 51 trường hợp 3 số đôi một khác nhau
- Nếu 3 chữ số A viết có 1 cặp giống nhau, tương ứng B sẽ có 2 cách viết \(\Rightarrow\) có \(3.2=6\) cách
- Nếu 3 chữ số A viết đôi một khác nhau, ứng với mỗi số B có 4 cách viết \(\Rightarrow51.4=204\) cách
\(\Rightarrow\) Ở trường hợp này có \(204+6=210\) cách
TH3: \(\overline{abc}\) không chứa số 0 nào
TH3.1: 3 chữ số a;b;c giống nhau \(\Rightarrow\) A có 9 cách viết, ứng với 1 số B cũng chỉ có 1 cách duy nhất \(\Rightarrow\) có 9 cách
TH3.2: 3 chữ số a;b;c có đúng 1 cặp giống nhau \(\Rightarrow\) a;b;c cùng số dư khi chia cho 3.
Có 9 cách chọn 1 cặp số giống nhau, với mỗi cặp sẽ có 2 cách chọn số còn lại \(\Rightarrow\) 18 cách chọn. Với mỗi số lại có 3 cách hoán vị \(\Rightarrow18.3=54\) cách để A viết
Với mỗi số A viết, B có 3 cách viết tương ứng
\(\Rightarrow\) có \(54.3=162\) cách
TH3.3: 3 chữ số a;b;c đôi một khác nhau:
- Cả 3 số đều chia hết cho 3 \(\Rightarrow\) \(1.3!=6\) cách
- Cả 3 số chia 3 cùng số dư: \(2.3!=12\) cách
- 1 số chia 3 dư 1, 1 số chia 3 dư 2, 1 số chia hết cho 3: có \(3.3.3.3!=162\) cách
\(\Rightarrow\) có \(6+12+162=180\) cách để A viết
Với mỗi số A viết, B có \(3!=6\) cách viết tương ứng
\(\Rightarrow\) Có \(180.6=1080\) cách
Vậy tổng cộng có: \(3+210+9+162+1080=1464\) cách viết
Phức tạp quá nên chẳng biết có thiếu chỗ nào ko :D

Gọi số Xuân viết là A
A1994 = A+11993
10000.A + 1994 = A + 11993
9999.A=9999
A=1
Mỗi bạn có 16 cách viết nên số phần tử không gian mẫu là 16^3.
Gọi A là biến cố '3 số được viết ra có tổng chia hết cho 3'
Các số tự nhiên từ 1 đến 16 chia thành 3 nhóm:
Nhóm I gồm các số tự nhiên chia hết cho 3 gồm 5 số.
Nhóm II gồm các số tự nhiên cho 3 dư 1 gồm 6 số.
Nhóm III gồm các số tự nhiên cho 3 dư 2 gồm 5 số.
Để ba số có tổng chia hết cho 3 thì xảy ra các trường hơp sau:
Cả ba bạn viết được số thuộc nhóm I có 5^3 cách.
Cả ba bạn viết được số thuộc nhóm II có 6^3 cách.
Cả ba bạn viết được số thuộc nhóm III có 5^3 cách.
Mỗi bạn viết được một số thuộc một nhóm có 3!×(5×6×5)
=> n(A) = 5^3 + 6^3 + 5^3 + 3!×(5×6×5) = 1366
Vậy P(A) = 1366/16^3