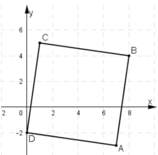
Tronng mặt phẳng Oxy, cho hình vuông ABCD có A(1;-1) và B(3;0).Tọa độ các đỉnh C và D là:
A.C(4;-2);D(2;2) hoặc C(2;-4);D(4;-2)
B.C(4;2);D(2;-3) hoặc C(-2;2);D(0;1)
C.C(4;-2);D(2;3) hoặc C(2;2);D(0:1)
D.C(2;-3);D(0;1) hoặc C(0;1);D(2;-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 8 2018
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
Trong mặt phẳng Oxy, cho hình vuông ABCD có đình M(-–-3;5), tâm I thuộc đường thẳng d : y =−x+5 và diện tích của hình vuông ABCD bằng 25 . Tim tọa độ các đỉnh của hình vuông ABCD, biết rằng tâm I có hoành độ dương
CM
1 tháng 3 2018
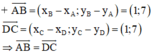
⇒ ABCD là hình bình hành.
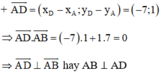
⇒ hình bình hành ABCD là hình chữ nhật.
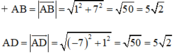
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).
Gọi \(D\left(x;y\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2;1\right)\\\overrightarrow{AD}=\left(x-1;y+1\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AB=\sqrt{5}\\AD=\sqrt{\left(x-1\right)^2+\left(y+1\right)^2}\end{matrix}\right.\)
Do ABCD là hình vuông nên:
\(\left\{{}\begin{matrix}\overrightarrow{AB}.\overrightarrow{AD}=0\\AB=AD\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2\left(x-1\right)+y+1=0\\\left(x-1\right)^2+\left(y+1\right)^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left(x-1\right)^2+4\left(x-1\right)^2=5\)
\(\Leftrightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=2\Rightarrow y=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}D\left(0;1\right)\\D\left(2;-3\right)\end{matrix}\right.\)
Với \(D\left(0;1\right)\Rightarrow\overrightarrow{DC}=\overrightarrow{AB}\Rightarrow C\left(2;2\right)\)
Cả 4 đáp án đều sai