cho hình thang ABCD có độ dài đáy lớn AB bằng 2 lần đáy nhỏ CD gọi I là trung điểm AB. Đường thẳng AD cắt BC tại E .
a) chứng minh AICD và BCDI là hình bình hành
b) chứng minh AD = DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
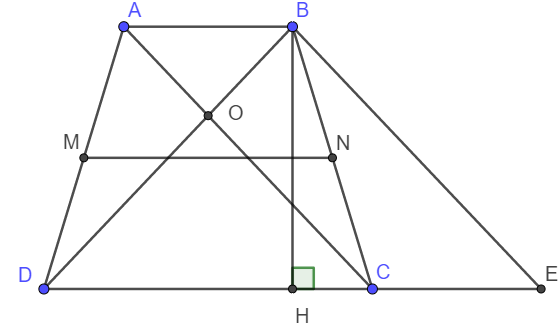
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.
11 tháng 10 2021
\(a,\left\{{}\begin{matrix}AE=ED\\BF=FC\end{matrix}\right.\Rightarrow EF\) là đtb hthang ABCD
\(\Rightarrow EF=\dfrac{AB+CD}{2};EF//AB//CD\left(đpcm\right)\)
\(b,\left\{{}\begin{matrix}BF=FC\\FK//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow AK=KC\) hay BK là trung tuyến tg ABC
\(c,\left\{{}\begin{matrix}AE=ED\\EI//AB\left(EF//AB\right)\end{matrix}\right.\Rightarrow BI=ID\Rightarrow IE\) là đtb tg ABD
\(\Rightarrow IE=\dfrac{1}{2}AB.hay.AB=2IE\)
\(d,\left\{{}\begin{matrix}BF=FC\\AK=KC\end{matrix}\right.\Rightarrow FK\) là đtb tg ABC
\(\Rightarrow FK=\dfrac{1}{2}AB=IE\left(đpcm\right)\)
\(e,\) Ta có \(FK=IE=\dfrac{AB}{2}=3\)
\(KF=EF-EI-FK=\dfrac{AB+CD}{2}-3-3=8-3-3=2\)
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Như - Toán lớp 8 - Học toán với OnlineMath
