Cho phương trình : cos2x+4cosx+m=0 . Tìm tẩ cả các giá trị tham số m để phương trình đã cho có nghiệm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 2 2018
Đáp án D
t 2 − 4 t + m = 0 Δ ' = 4 − m ≥ 0 ⇔ m ≤ 4 t = 2 ± 4 − m ⇒ 2 − 4 − m ≤ 1 2 + 4 − m ≤ 1 ⇔ 1 ≤ 4 − m ≤ 3 ⇔ − 5 ≤ m ≤ 3
NC
0
CM
7 tháng 6 2018
Đáp án A
Phương pháp:
Cô lập m, đưa về dạng f(x) = m
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Điều kiện: x ≠ 2, x ≠ -4
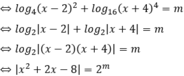
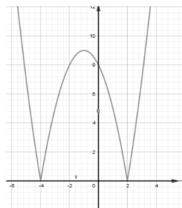
Số nghiệm của phương trình đã cho bằng số giao điểm của đồ thị hàm số y = |x2 + 2x - 8| và đường thẳng y = 2m
Quan sát đồ thị hàm số bên, ta thấy, để đồ thị hàm số y = |x2 + 2x - 8| cắt đường thẳng y = 2m tại 4 điểm phân biệt thì 0 < 2m < 9 ⇔ m < log29 ⇔ m < 2 log23
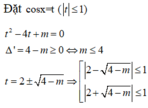
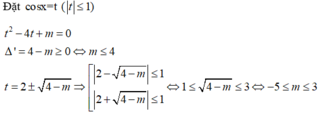
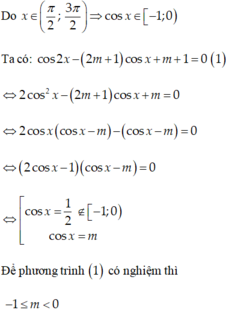
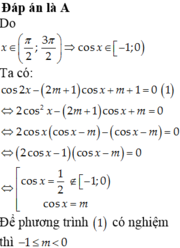
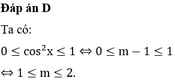
\(\Leftrightarrow2cos^2x+4cosx-1=-m\)
Xét \(f\left(x\right)=2cos^2x+4cosx-1\)
\(f\left(x\right)=2cos^2x+4cosx+2-3=2\left(cosx+1\right)^2-3\ge-3\)
\(f\left(x\right)=2cos^2x+4cosx-6+5=2\left(cosx-1\right)\left(cosx+3\right)+5\le5\)
\(\Rightarrow-3\le-m\le5\Rightarrow-5\le m\le3\)