Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Bạn tự giải
b. Pt hoành độ giao điểm: \(x^2=mx-m+1\Leftrightarrow x^2-mx+m-1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1-m\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=m-1\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x_1=1\\x_2=m-1\end{matrix}\right.\) \(\Rightarrow1=9\left(m-1\right)\Rightarrow m=\dfrac{10}{9}\)
TH2: \(\left\{{}\begin{matrix}x_1=m-1\\x_2=1\end{matrix}\right.\) \(\Rightarrow m-1=9.1\Rightarrow m=10\)

\(\left(d\right)\) cắt \(\left(P\right)\) tại 2 điểm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow\left(2m+5\right)^2+4\left(2m+6\right)>0\)
\(\Leftrightarrow4m^2+20m+25+8m+24>0\)
\(\Leftrightarrow\left(2m+7\right)^2>0\) (luôn đúng)
Viet \(\left\{{}\begin{matrix}x_1+x_2=2m+5\\x_1x_2=-2m-6\end{matrix}\right.\)
\(\left|x_1\right|+\left|x_2\right|=7\)\(\Leftrightarrow\left(x_1+x_2\right)^2=7^2\)
\(\Leftrightarrow\left(2m+5\right)^2=49\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-6\\m=1\end{matrix}\right.\)
-Chúc bạn học tốt-

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
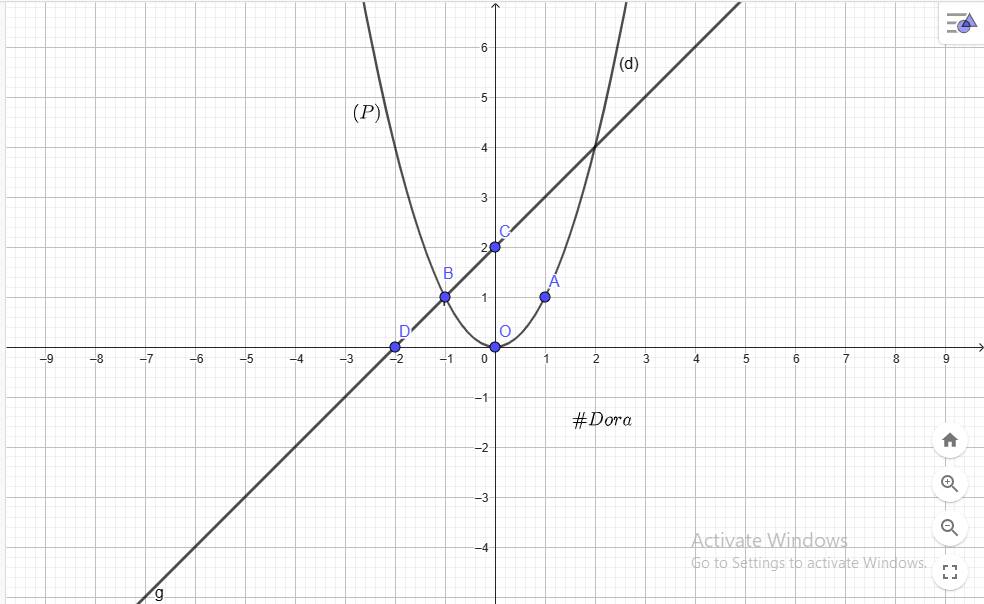
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4

a: PTHĐGĐ là;
x^2-(2m-3)x+m^2-3m=0
Δ=4m^2-12m+9-4m^2+12m=9>0
=>(P) luôn cắt (d) tại hai điểm pb
b: |x1|+|x2|=3
=>x1^2+x2^2+2|x1x2|=9
=>(2m-3)^2-2(m^2-3m)+2|m^2-3m|=9
TH1: m>=3 hoặc m<=0
=>(2m-3)^2=9
=>m=3(nhận) hoặc m=0(nhận)
Th2: 0<m<3
=>4m^2-12m+9-4(m^2-3m)=9
=>4m^2-12m-4m^2+12m=0
=>0m=0(luôn đúng)

Phương trình hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)
a. Khi \(m=-1\), (1) trở thành:
\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)
b.
\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) cắt (P) tại 2 điểm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)
\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)